(本小题满分12分)为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
| 处罚金额x(单位:元) |
0 |
5 |
10 |
15 |
20 |
| 会闯红灯的人数y |
80 |
50 |
40 |
20 |
10 |
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
(本小题满分10分)
已知向量: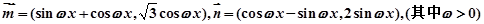 ,函数
,函数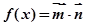 ,若
,若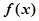 相邻两对称轴间的距离为
相邻两对称轴间的距离为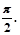
(Ⅰ)求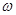 的值,并求
的值,并求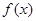 的最大值及相应x的集合;
的最大值及相应x的集合;
(Ⅱ)在△ABC中,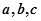 分别是A,B,C所对的边,△ABC的面积
分别是A,B,C所对的边,△ABC的面积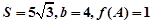 ,求边
,求边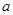 的长。
的长。
已知函数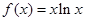 ,
, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若对任意正实数x,不等式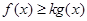 恒成立,求实数k的值;
恒成立,求实数k的值;
(Ⅲ)求证: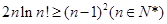 .(其中
.(其中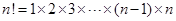 )
)
如图,已知抛物线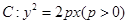 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.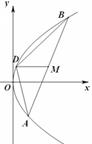
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线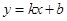 与抛物线C交于两点
与抛物线C交于两点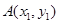 ,
,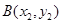 ,且
,且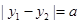 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到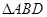 .
.
(i)求实数a,b,k满足的等量关系;
(ii)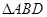 的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
如图,在组合体中,ABCD—A1B1C1D1是一个长方体,P—ABCD是一个四棱锥.AB=2,BC=3,点P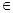 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD=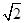 .
.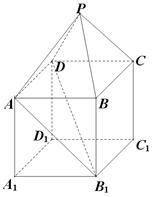
(1)证明:PD 平面PBC;
平面PBC;
(2)求PA与平面ABCD所成的角的正切值;
(3)若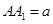 ,当a为何值时,PC//平面
,当a为何值时,PC//平面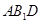 .
.
(本题13分)
如图,在四棱锥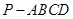 中,
中,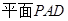
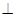 平面
平面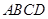 ,底面
,底面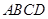 是菱形,
是菱形,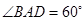 .
.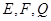 分别是
分别是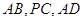 的中点.
的中点.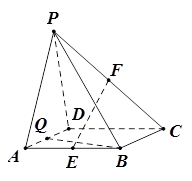
(1) 求证: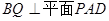 ;
;
(2) 求证: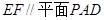 .
.