选修4-4:极坐标与参数方程
在直角坐标系xOy中,圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2交点的极坐标;
(Ⅱ)求圆C1与C2的公共弦的参数方程.
一袋中装有4个形状、大小完全相同的球,其中黑球2个,白球2个,假设每个小球从袋中被取出的可能性相同,首相由甲取出2个球,并不在将他们原袋中,然后由乙取出剩下的2个球.规定取出一个黑球记1分,取出一个白球记2分,取出球的总积分多者获胜.
(1)求甲、乙平局的概率;
(2)假设可以选择取球的先后顺序,应选择先取,还是后取,请说明理由.
设函数
(1)求函数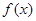 的最小正周期;
的最小正周期;
(2)若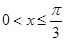 ,求
,求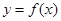 的值域.
的值域.
已知函数 在
在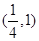 上的最大值为
上的最大值为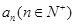
求数列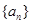 的通项公式;
的通项公式;
求证:对任何正整数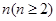 ,都有
,都有 ;
;
设数列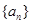 的前
的前 项和
项和 ,求证:对任何正整数
,求证:对任何正整数 ,都有
,都有 成立
成立
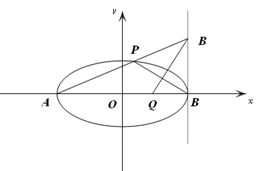
已知椭圆 ,过点
,过点 且离心率为
且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)已知 是椭圆
是椭圆 的左右顶点,动点M满足
的左右顶点,动点M满足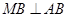 ,连接AM交椭圆于点P,在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.
,连接AM交椭圆于点P,在x轴上是否存在异于A、B的定点Q,使得直线BP和直线MQ垂直.
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥 与
与 ,且
,且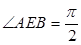 .
.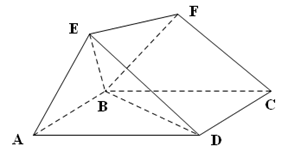
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面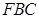 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.