如图,已知抛物线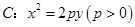 ,其焦点
,其焦点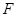 到准线的距离为
到准线的距离为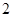 ,点
,点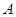 、点
、点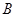 是抛物线
是抛物线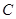 上的定点,它们到焦点
上的定点,它们到焦点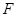 的距离均为
的距离均为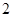 ,且点
,且点 位于第一象限.
位于第一象限.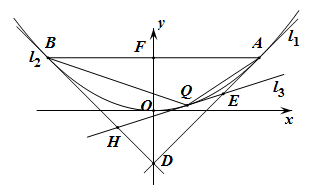
(1)求抛物线 的方程及点
的方程及点 、点
、点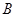 的坐标;
的坐标;
(2)若点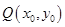 是抛物线
是抛物线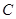 异于
异于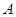 、
、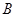 的一动点,分别以点
的一动点,分别以点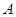 、
、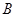 、
、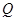 为切点作抛物线
为切点作抛物线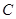 的三条切线
的三条切线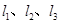 ,若
,若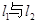 、
、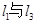 、
、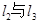 分别相交于D、E、H,设
分别相交于D、E、H,设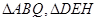 的面积依次为
的面积依次为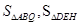 ,记
,记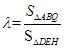 ,问:
,问: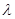 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
近年来,网上购物已经成为人们消费的一种趋势。假设某淘宝店的一种装饰品每月的销售量y(单位:千件)与销售价格x(单位:元/件)满足关系式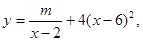 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值;(2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值;(2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
已知向量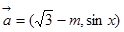 ,
,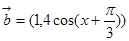 ,(
,(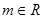 ,且
,且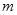 为常数),设函数
为常数),设函数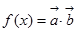 ,若
,若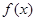 的最大值为1.
的最大值为1.
(1)求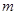 的值,并求
的值,并求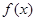 的单调递增区间;
的单调递增区间;
(2)在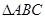 中,角
中,角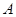 、
、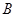 、
、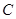 的对边
的对边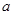 、
、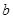 、
、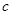 ,若
,若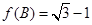 ,且
,且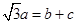 ,试判断三角形的形状.
,试判断三角形的形状.
已知数列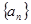 及其前
及其前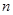 项和
项和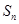 满足:
满足: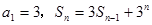 (
(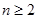 ,
, ).
).
(1)证明:设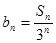 ,
,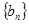 是等差数列;
是等差数列;
(2)求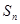 及
及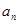 ;
;
(3)判断数列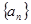 是否存在最大或最小项,若有则求出来,若没有请说明理由.
是否存在最大或最小项,若有则求出来,若没有请说明理由.
已知: 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 =(1,2)
=(1,2)
⑴若| |
|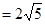 ,且
,且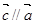 ,求
,求 的坐标;
的坐标;
⑵若| |=
|=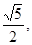 且
且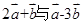 垂直,求
垂直,求 与
与 的夹角θ。
的夹角θ。
设函数
(1)当 时,求函数
时,求函数 的最大值;
的最大值;
(2)令 (
( )其图象上任意一点
)其图象上任意一点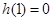 处切线的斜率
处切线的斜率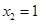 ≤
≤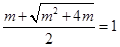 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当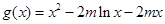 ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数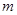 的值.
的值.