(本小题满分10分)如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,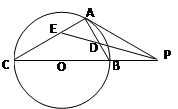
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求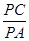 的值.
的值.
(本小题满分12分)设函数 ,其中
,其中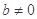 .
.
(Ⅰ)若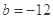 ,求
,求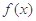 在
在 的最小值;
的最小值;
(Ⅱ)如果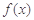 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(本小题满分12分)如图:三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= ,D是侧棱AA1的中点.
,D是侧棱AA1的中点.
(Ⅰ)证明:平面BDC1⊥平面BDC;
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.
(本小题满分12分)甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球, 编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.
(Ⅰ)求游戏Ⅰ中甲赢的概率;
(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.
(本小题满分12分)若函数 的图像与直线y="m" (m为常数)相切,并且切点的横坐标依次成等差数列,且公差为
的图像与直线y="m" (m为常数)相切,并且切点的横坐标依次成等差数列,且公差为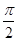 .
.
(Ⅰ)求m的值;
(Ⅱ)若点A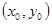 是y=f(x)图像的对称中心,且
是y=f(x)图像的对称中心,且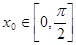 ,求点A的坐标.
,求点A的坐标.