出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:km)如下:
-2,+5,-1,+1,-6,-2,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为0.2L/km(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为3km(包括3km),超过部分每千米1.2元,问小李这天上午共得车费多少元?
如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题: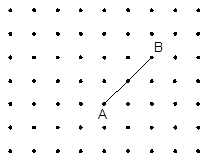
(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
两人要去某风景区游玩,每天某—时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆乍的状况比第一辆好,他就上第二辆车;如果第二辆不比第—辆好,他就上第三辆车.若把这三辆车的舒适程度分为上、中、下三等.请问:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
《列子》中《歧路亡羊》写道:
杨子之邻人亡羊,既率其党,又请杨子之竖追之。杨子曰:“嘻!亡一羊,何追者之众?”邻人日:“多歧路。”既反,问:“获羊乎?”日:“亡之矣。”曰:“奚亡之?”曰:“歧路之中又有歧焉,吾不知所之,所以反也.”
如图,假定所有的分叉口都各有两条新的歧路,并且丢失的羊走每条歧路的可能性都相等.
(1)到第n次分歧时,共有多少条歧路?以当羊走过n个三叉路口后,找到羊的概率是多少?
(2)当n=5时,派出6个人去找羊,找到羊的概率是多少?
小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回.
(1)若小明恰好抽到了黑桃4.①请在下边框中绘制这种情况的树状图;②求小华抽出的牌面数字比4大的概率.
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负.你认为这个游戏是否公平?说明你的理由.
将三根直径为a的圆柱形钢管用铁丝捆扎,现设计了两种方案,如图所示,请你探索,宜采用哪一种方案.

(1) (2)