如图1,已知:抛物线y= x2+bx+c与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是y=
x2+bx+c与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是y= x-2,连结AC.
x-2,连结AC.
(1)求出抛物线的函数关系式;
(2)若△ABC内部能否截出面积最大的矩形DEFC(顶点D、E、F、G在△ABC各边上)?若能,求出在AB边上的矩形顶点的坐标;若不能,请说明理由.
(3)点P(t,0)是x轴上一动点,P、Q两点关于直线BC成轴对称,PQ交BC于点M,作QH⊥x轴于点H.连结OQ,是否存在t的值,使△OQH与△APM相似?若存在,求出t的值;若不存在,说明理由.
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
①∠AEF=∠BCE;
②AF+BC>CF;
③S△CEF=S△EAF+S△CBE;
④若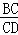 =
= ,则△CEF≌△CDF.
,则△CEF≌△CDF.
其中正确的结论是 .(填写所有正确结论的序号)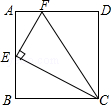
如图1,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟高.
(1)抛物线y= x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
(2)抛物线y=ax2﹣4ax﹣ (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
(3)将抛物线y=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3…),定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn,则hn= ,Fn的碟宽有端点横坐标为 2 ;F1,F2,…,Fn的碟宽右端点是否在一条直线上?若是,直接写出该直线的表达式;若不是,请说明理由.
如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B,C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依次操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围;
(3)若经过多次操作可得到首尾顺次相接的多边形,其最大边数是多少?它可能是正多边形吗?如果是,请直接写出其边长;如果不是,请说明理由.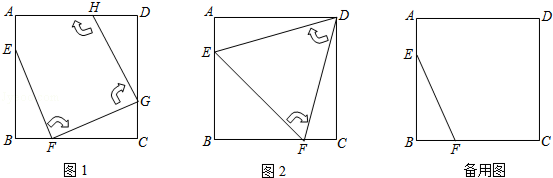
如图1,AB是⊙O的直径,点C在AB的延长线上,AB=4,BC=2,P是⊙O上半部分的一个动点,连接OP,CP.
(1)求△OPC的最大面积;
(2)求∠OCP的最大度数;
(3)如图2,延长PO交⊙O于点D,连接DB,当CP=DB时,求证:CP是⊙O的切线.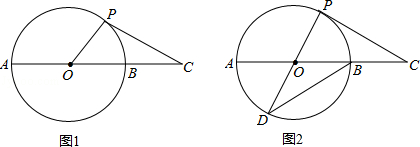
图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.
(1)连接CD,EB,猜想它们的位置关系并加以证明;
(2)求A,B两点之间的距离(结果取整数,可以使用计算器)
(参考数据: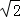 ≈1.41,
≈1.41,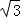 ≈1.73,
≈1.73,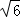 ≈2.45)
≈2.45)