(本小题满分10分)【选修4一1:几何证明选讲】
如图,已知圆的两条弦AB,CD,延长AB,CD交于圆外一点E,过E作AD的平行线交CB的延长线于F,过点F作圆的切线FG,G为切点.求证: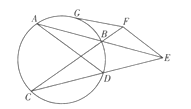
(1)△EFC∽△BFE;
(2)FG=FE.
(本小题满分14分)已知函数 处取得极值2.
处取得极值2.
(1)求函数 的解析式;
的解析式;
(2)实数m满足什么条件时,函数 在区间
在区间 上单调递增?
上单调递增?
(3)是否存在这样的实数m,同时满足:①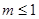 ;②当
;②当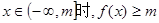 恒成立.若存在,请求出m的取值范围;若不存在,说明理由.
恒成立.若存在,请求出m的取值范围;若不存在,说明理由.
.(本小题满分14分)已知椭圆 的一个焦点
的一个焦点 与抛物线
与抛物线 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为
,倾斜角为 的直线
的直线 过点
过点 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为 ,试求抛物线
,试求抛物线 上一点
上一点 ,使得
,使得 与
与 关于直线
关于直线 对称,求出点
对称,求出点 的坐标.
的坐标.
(本小题满分14分)
已知函数
(1)求函数 在点(1,f(1))处的切线方程.
在点(1,f(1))处的切线方程.
(2)求函数 的单调区间和极值.
的单调区间和极值.
(本小题满分14分)
已知椭圆E的两个焦点分别为F1(-1,0), F2 (1,0), 点(1,  )在椭圆E上.
)在椭圆E上.
(1)求椭圆E的方程
(2)若椭圆E上存在一点 P, 使∠F1PF2=30°, 求△PF1F2的面积.
(本小题满分12分)
某中学采取分层抽样的方法从应届高三学生中按照性别抽取20名学生,
其中8名女生中有3名报考理科,男生中有2名报考文科
(1)是根据以上信息,写出 列联表
列联表
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?参考公式
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
 |
2.07 |
2.71 |
3.84 |
5.02 |
6.64 |
7.88 |
10.83 |