已知以向量v= 为方向向量的直线l过点
为方向向量的直线l过点 ,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
,抛物线C:y2=2px(p>0)的顶点关于直线l的对称点在该抛物线的准线上.
(1)求抛物线C的方程;
(2)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m,直线OB与直线m交于点N,若 ·
· +p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
+p2="0" (O为原点,A、B异于原点),试求点N的轨迹方程.
已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点A(m,-3)到焦点F的距离为5,求m的值,并写出此抛物线的方程.
已知点N(1,2),过点N的直线交双曲线x2- =1于A、B两点,且
=1于A、B两点,且 =
= (
( +
+ ).
).
(1)求直线AB的方程;
(2)若过N的直线交双曲线于C、D两点,且 ·
· =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?
已知定点A(0,7)、B(0,-7)、C(12,2),以C为一个焦点作过A、B的椭圆,求另一焦点F的轨迹方程.
如图所示,设抛物线方程为x2="2py" (p>0),M为直线y=-2p上任意一点,过M 引抛物线的切线,切点分别为A,B.
引抛物线的切线,切点分别为A,B.
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为(2,-2p)时,|AB|=4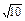 .求此时抛物线的方程.
.求此时抛物线的方程.