如图，在凸四边形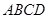
中，
为定点，
,
为动点，满足
．
（1）写出
与
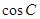的关系式；
（2）设△BCD和△ABD的面积分别为
和
，求
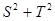的最大值．
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为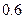
，被甲或乙解出的概率为
，（1）求该题被乙独立解出的概率；（2）求解出该题的人数
的数学期望和方差
要制造一种机器零件，甲机床废品率为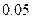
，而乙机床废品率为
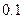，而它们
的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：
（1）其中至少有一件废品的概率；（2）其中至多有一件废品的概率.
三个元件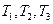
正常工作的概率分别为
将它们中某两个元件并联后再和第三元件串联接入电路.
（Ⅰ）在如图的电路中，电路不发生故障的概率是多少？
|
（Ⅱ）三个元件连成怎样的电路，才能使电路中不发生故障的概率最大？请画出此时电路图，并说明理由.
某学生语、数、英三科考试成绩，在一次考试中排名全班第一的概率：语文为
，
数学为
，英语为
，问一次考试中
（Ⅰ）三科成绩均未获得第一名的概率是多少？
（Ⅱ）恰有一科成绩未获得第一名的概率是多少
奖器有
个小球，其中
个小球上标有数字
，个小球上标有数字
，现摇出
个小球，规定所得奖金（元）为这个小球上记号之和，求此次摇奖获得奖金数额的数学期望
