(本小题13分)已知数列{an}的前n项和是Sn,且Sn+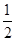 an=1.
an=1.
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1),求适合方程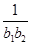 +
+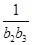 +…+
+…+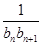 =
=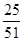 的n的值.
的n的值.
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)已知正项等比数列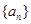 满足:
满足: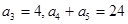 .
.
(Ⅰ)求数列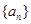 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列 的前
的前 项和
项和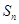 .
.
如图,已知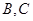 是以原点
是以原点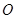 为圆心,半径为
为圆心,半径为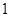 的圆与
的圆与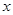 轴的交点,点
轴的交点,点 在劣弧
在劣弧 (包含端点)上运动,其中
(包含端点)上运动,其中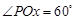 ,
,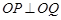 ,作
,作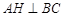 于
于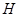 .若记
.若记 ,则
,则 的取值范围是
的取值范围是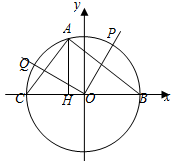
A.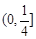 |
B. |
C. |
D.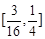 |
(本题共12分,第(Ⅰ)问4分, 第(Ⅱ)问8分)已知数列 满足:
满足:
 .
.
(Ⅰ)若 ,
,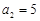 ,
,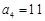 ,求
,求 的值;
的值;
(Ⅱ)若 ,证明:
,证明: 且
且 ,
, .
.
(本题共12分,第(Ⅰ)问4分,第(Ⅱ)问8分)设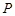 为圆
为圆 上的动点,过
上的动点,过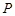 作
作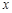 轴的垂线,垂足为
轴的垂线,垂足为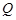 ,点
,点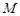 满足:
满足: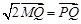 .
.
(Ⅰ)求点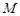 的轨迹
的轨迹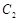 的方程;
的方程;
(Ⅱ)过直线 上的点
上的点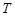 作圆
作圆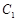 的两条切线,设切点分别为
的两条切线,设切点分别为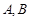 ,若直线
,若直线 与点
与点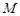 的轨迹
的轨迹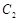 交于
交于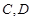 两点,若
两点,若 ,求实数
,求实数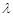 的取值范围.
的取值范围.
(本题共12分,第(Ⅰ)问6分,第(Ⅱ)问6分)如图所示,已知三棱柱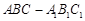 ,点
,点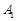 在底面
在底面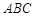 上的射影恰为
上的射影恰为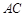 的中点
的中点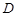 ,
,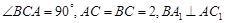 .
.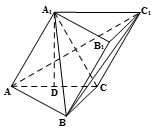
(Ⅰ)求证: 平面
平面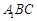 ;
;
(Ⅱ)求二面角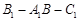 的余弦值.
的余弦值.