(本小题满分12分)某公司利用A、B两种原料生产甲、乙两种产品,每生产1吨产品所需要的原料及利润如下表所示:
| |
A种原料(单位:吨) |
B种原料(单位:吨) |
利润(单位:万元) |
| 甲种产品 |
1 |
2 |
3 |
| 乙种产品 |
2 |
1 |
4 |
公司在生产这两种产品的计划中,要求每种产品每天消耗A、B原料都不超过12吨.求每天生产甲、乙两种产品各多少吨,使公司获得总利润最大?最大利润是多少?
(本题满分14分)设等比数列 的首项为
的首项为 ,公比
,公比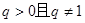 ,前
,前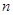 项和为
项和为
(Ⅰ)当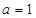 时,
时, 三数成等差数列,求数列
三数成等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数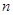 ,命题甲:
,命题甲: 三数构成等差数列.
三数构成等差数列.
命题乙: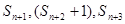 三数构成等差数列.
三数构成等差数列.
求证:对于同一个正整数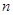 ,命题甲与命题乙不能同时为真命题.
,命题甲与命题乙不能同时为真命题.
(本题满分14分)设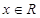 ,向量
,向量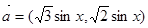 ,
,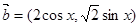 ,函数
,函数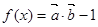 .(Ⅰ)在区间
.(Ⅰ)在区间 内,求
内,求 的单调递减区间;
的单调递减区间;
(Ⅱ)若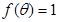 ,其中
,其中 ,求
,求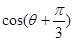 .
.
设 x1、x2(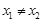 )是函数
)是函数  (
( )的两个极值点.(I)若
)的两个极值点.(I)若 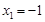 ,
,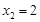 ,求函数
,求函数  的解析式;
的解析式;
(II)若 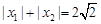 ,求 b 的最大值;
,求 b 的最大值;
(III)设函数 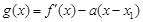 ,
,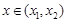 ,当
,当 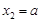 时,求
时,求 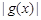 的最大值.
的最大值.
设椭圆 C1: (
( )的一个顶点与抛物线 C2:
)的一个顶点与抛物线 C2: 的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率
的焦点重合,F1,F2 分别是椭圆的左、右焦点,离心率  ,过椭圆右焦点 F2 的直线
,过椭圆右焦点 F2 的直线  与椭圆 C 交于 M,N 两点.
与椭圆 C 交于 M,N 两点.
(I)求椭圆C的方程;
(II)是否存在直线  ,使得
,使得  ,若存在,求出直线
,若存在,求出直线  的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(III)若 AB 是椭圆 C 经过原点 O 的弦,MN//AB,求证: 为定值.
为定值.
(本小题满分14分)数列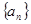 满足
满足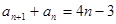
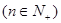 .
.
(Ⅰ)若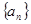 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若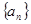 满足
满足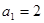 ,
,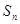 为
为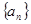 的前
的前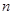 项和,求
项和,求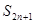 .
.