已知直线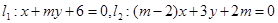
，求
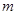的值，使得
（1）
；
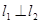（2）
∥
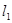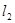
假设你家订了一份报纸，送报人可能在早上6:30～7:30之间把报纸送到你家，你父亲离开家去工作的时间在早上7:00～8:00之间，现在利用随机模拟试验的方法，设送报人送到的时间为
，你父亲去上班的时间为
，通过计算机产生如下20组数据，根据这20组数据，求你父亲在离开家前能得到报纸的概率是多少？
| 序号 |
x的值 |
y的值 |
| 1 |
6.9877 |
7.8705 |
| 2 |
7.4551 |
7.8306 |
| 3 |
7.2142 |
7.1536 |
| 4 |
7.1956 |
7.8930 |
| 5 |
7.3802 |
7.3392 |
| 6 |
7.1752 |
7.6632 |
| 7 |
6.9864 |
7.5624 |
| 8 |
6.9376 |
7.8601 |
| 9 |
6.7595 |
7.7660 |
| 10 |
6.8464 |
7.3132 |
| 11 |
7.4267 |
7.7279 |
| 12 |
6.9119 |
7.4720 |
| 13 |
6.5753 |
7.2793 |
| 14 |
7.0090 |
7.7624 |
| 15 |
7.4258 |
7.4488 |
| 16 |
7.3529 |
7.2884 |
| 17 |
7.0754 |
7.8694 |
| 18 |
7.2386 |
7.2847 |
| 19 |
7.1166 |
7.8057 |
| 20 |
7.4023 |
7.3700 |
已知圆的方程为
，直线方程为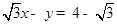
求（Ⅰ）圆心到直线的距离
；
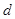（Ⅱ）直线被圆所截得的弦长.
已知
是函数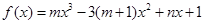
的一个极值点，其中
，
（I）求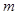
与
的关系式；
（II）求
的单调区间；
（III）当
时，函数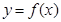
的图象上任意一点的切线斜率恒大于3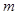，求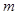的取值范围.
如图，已知椭圆
的离心率为
，且经过点
平行于
的直线
在
轴上的截距为
，与椭圆有A、B两个
不同的交点
（Ⅰ） 求椭圆的方程；
(Ⅱ)求
的取值范围；
（III）求证:直线
、
与
轴始终围成一个等腰三角形．
若数列
的前
项和为
：；
（Ⅰ） 求数列的通项公式
；
(Ⅱ) 设数列
的前项和为
，是否存在实数
，使得
对一切正整数都成立?若存在,求出的最小值,若不存在,请说明理由．