(本小题满分12分) 设函数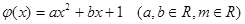
(1)若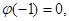 且对任意实数
且对任意实数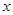 均有
均有 成立,求实数
成立,求实数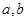 的值;
的值;
(2)在(1)的条件下,令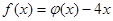 ,若
,若 与
与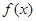 在
在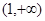 上有相同的单调性,
上有相同的单调性,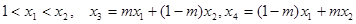 且
且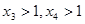 ,试比较
,试比较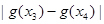 与
与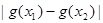 的大小
的大小
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,(i)摸出3个白球的概率;(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数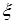 的分布列及数学期望
的分布列及数学期望 .
.
在 中,已知内角
中,已知内角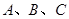 所对的边分别为
所对的边分别为 ,向量
,向量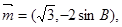
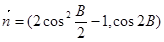 ,且
,且 //
//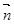 ,
,  为锐角.
为锐角.
(1)求角 的大小;(2)设
的大小;(2)设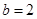 ,求
,求 的面积
的面积 的最大值.
的最大值.
已知 在
在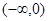 上是增函数,在
上是增函数,在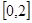 上是减函数,且方程
上是减函数,且方程 有三个根,它们分别为
有三个根,它们分别为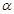 ,2,
,2,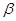 .
.
(Ⅰ)求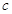 的值;(Ⅱ)求证:
的值;(Ⅱ)求证: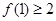 ;(Ⅲ)求
;(Ⅲ)求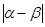 的取值范围.
的取值范围.
设椭圆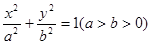 的左焦点为
的左焦点为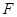 ,上顶点为
,上顶点为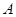 ,过点
,过点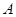 与
与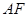 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和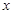 轴正半轴于
轴正半轴于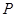 ,
,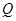 两点,且
两点,且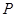 分向量
分向量 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过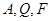 三点的圆恰好与直线
三点的圆恰好与直线 :
: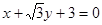 相切,求椭圆方程.
相切,求椭圆方程.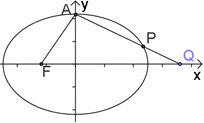
数列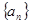 中,
中, 且满足
且满足

⑴求数列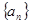 的通项公式;
的通项公式;
⑵设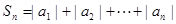 ,求
,求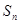 ;
;
⑶设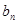 =
=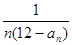
 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意
,使得对任意 ,均有
,均有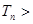
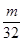 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。