如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.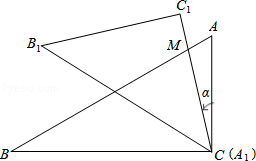
(1)计算A1C1的长;
(2)当α=30°时,证明:B1C1∥AB;
(3)若a=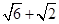 ,当α=45°时,计算两个三角板重叠部分图形的面积;
,当α=45°时,计算两个三角板重叠部分图形的面积;
(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(参考数据:sin15°=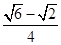 ,cos15°=
,cos15°=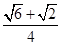 ,tan15°=2-
,tan15°=2-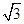 ,sin75°=
,sin75°=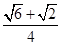 ,cos75°=
,cos75°=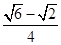 ,tan75°=2+
,tan75°=2+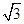 )
)
(凉山州)在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数 的图象上的概率;
的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
(凉山州)阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF= (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
请你运用所学知识,结合上述材料,解答下列问题.
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD= ,OC=5,求MN的长.
,OC=5,求MN的长.
(凉山州)如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.
(1)求证:PA•PB=PD•PC;
(2)若PA= ,AB=
,AB=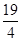 ,PD=DC+2,求点O到PC的距离.
,PD=DC+2,求点O到PC的距离.
(凉山州)如图,已知抛物线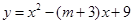 的顶点C在x轴正半轴上,一次函数
的顶点C在x轴正半轴上,一次函数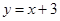 与抛物线交于A、B两点,与x、y轴交于D、E两点.
与抛物线交于A、B两点,与x、y轴交于D、E两点.
(1)求m的值.
(2)求A、B两点的坐标.
(3)点P(a,b)(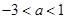 )是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
)是抛物线上一点,当△PAB的面积是△ABC面积的2倍时,求a,b的值.
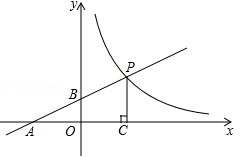
(资阳)如图,直线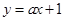 与x轴、y轴分别相交于A、B两点,与双曲线
与x轴、y轴分别相交于A、B两点,与双曲线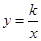 (
( )相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.