(本小题满分12分)已知函数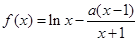 .
.
(Ⅰ)若函数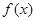 在
在 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(Ⅱ)设 ,且
,且 ,求证:
,求证: .
.
(本小题满分13分)
已知函数
(I)求函数 的通项公式;
的通项公式;
(Ⅱ)设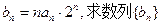 的前n项和Sn。
的前n项和Sn。
(本小题满分13分)
已知函数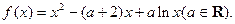
(I)求函数 的单调区间;
的单调区间;
(II)若 有三个交点,求m的取值范围(其中自然对数的底数e为无理数且
有三个交点,求m的取值范围(其中自然对数的底数e为无理数且 )
)
(本小题满分12分)
已知P在矩形ABCD边DC上,AB=2,BC=1,F在AB上且DF ⊥AP,垂足为E,将△ADP沿AP折起.使点D位于D′位置,连D′B、D′C得四棱锥D′—ABCP.
(I)求证D′F⊥AP;
|
(II)若PD=1并且平面D′AP⊥平面ABCP,求四棱锥D′—ABCP的体积
(本大题满分12分)
某班级共有60名学生.先用抽签法从中抽取部分学生调查他们的学习情况,若每名学生被抽到的概率为 。
。
(I)求从中抽取的学生数,
(Ⅱ)若抽查结果如下表
| 每周学习时间(小时) |
 |
 |
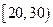 |
 |
| 人数 |
2 |
4 |
 |
1 |
先确定x,再完成频率分布直方图;
|
(III)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表)
本大题满分12分)
在△ABC中,
(I)求B,
(Ⅱ)若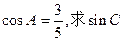 的值。
的值。