某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度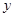 (单位:毫克/立方米)随着时间
(单位:毫克/立方米)随着时间 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为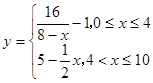 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求 的最小值(精确到
的最小值(精确到 ,参考数据:
,参考数据: 取
取 ).
).
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦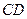 的延长线相交于点
的延长线相交于点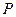 ,
,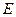 为⊙
为⊙ 上一点,AE=AC ,
上一点,AE=AC ,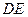 交
交 于点
于点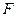 ,且
,且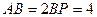 ,
,
(1)求 的长度.
的长度.
(2)若圆F且与圆 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下,
甲运动员
| 射击环数 |
频数 |
频率 |
| 7 |
10 |
0.1 |
| 8 |
10 |
0.1 |
| 9 |
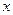 |
0.45 |
| 10 |
35 |
 |
| 合计 |
100 |
1 |
乙运动员
| 射击环数 |
频数 |
频率 |
| 7 |
8 |
0.1 |
| 8 |
12 |
0.15 |
| 9 |
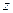 |
|
| 10 |
0.35 |
|
| 合计 |
80 |
1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
(3)若甲运动员射击2次,乙运动员射击1次,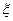 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求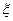 的分布列及
的分布列及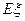 .
.
设 的内角
的内角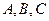 所对的边分别为
所对的边分别为 且
且 .
.
(1)求角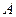 的大小;
的大小;
(2)若 ,求
,求 的周长
的周长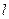 的取值范围.
的取值范围.
设函数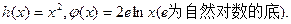 (1)求函数
(1)求函数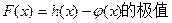 ; (2)若存在常数k和b,使得函数
; (2)若存在常数k和b,使得函数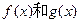 对其定义域内的任意实数
对其定义域内的任意实数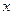 分别满足
分别满足 则称直线
则称直线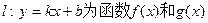 的“隔离直线”.试问:函数
的“隔离直线”.试问:函数 是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.
是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.
已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.(1)若线段AB中点的横坐标是- ,求直线AB的方程;(2)在x轴上是否存在点M,使
,求直线AB的方程;(2)在x轴上是否存在点M,使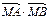 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.