已知 :
: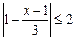 ;
; 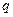 :
: ,若
,若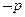 是
是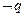 的必要而不充分条件,求实数a的取值范围 。
的必要而不充分条件,求实数a的取值范围 。
已知实数a,b∈{-2,-1,1,2}。
(1)求直线y=ax+b不经过第四象限的概率;
(2)求直线y=ax+b与圆x2+y2=1有公共点的概率。
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110。
(1)将这两组数据用茎叶图表示
(2)将两组数据比较,说明哪个车间产品较稳定。
(本小题满分14分)已知函数 在(0,+
在(0,+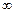 )上是增函数,在[–1,0]上是减函数,且方程
)上是增函数,在[–1,0]上是减函数,且方程 有三个根,它们分别为α,–1,β.
有三个根,它们分别为α,–1,β.
(1)求c的值;
(2)求证: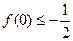 ;
;
(3)求|α–β|的取值范围.
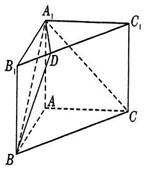
(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中,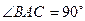 ,
,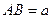 ,
, ,
,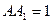 ,点D在棱
,点D在棱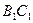 上,且
上,且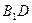 ∶
∶ ∶3
∶3
(1)证明:无论a为任何正数,均有BD⊥A1C;
(2)当a为何值时,二面角B—A1D—B1为60°?