已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标.
如图所示,四边形ABCD的对角线AC,BD相交于点O,△ABC≌△BAD.
求证:(1)OA=OB;(2)AB∥CD.
某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.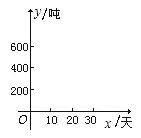
(1)分别求出甲、乙两条生产线各自总产量 (吨)与从乙开始投产以来所用时间
(吨)与从乙开始投产以来所用时间 (天)之间的函数关系式.
(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为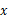 cm,则
cm,则 应是
应是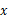 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| 第一套 |
第二套 |
|
椅子高度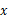 (cm) (cm) |
40 |
37 |
课桌高度 (cm) (cm) |
75 |
70 |
(1)请确定 与
与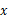 的函数关系式.
的函数关系式.
(2)现有一把高39 cm的椅子和一张高78.2 cm的课桌,它们是否配套?为什么?
已知 与
与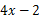 成正比例,且当
成正比例,且当 时,
时,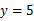 .
.
(1)求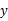 与
与 的函数关系式;
的函数关系式;
(2)求当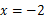 时的函数值.
时的函数值.
若一次函数 的图象与
的图象与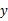 轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.
轴交点的纵坐标为-2,且与两坐标轴围成的直角三角形面积为1,试确定此一次函数的表达式.