(本小题满分12分)某工厂生产某种产品,每日的成本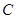 (单位:万元)与日产量(单位:吨)满足函数关系式
(单位:万元)与日产量(单位:吨)满足函数关系式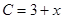 ,每日的销售
,每日的销售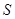 (单位:万元)与日产量的函数关系式为
(单位:万元)与日产量的函数关系式为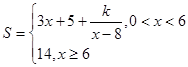 ,已知每日的利润
,已知每日的利润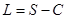 ,且当
,且当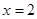 时,
时,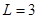 .
.
(1)求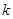 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求此最大值.
(本小题14分)已知点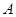 ,
,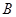 的坐标分别为
的坐标分别为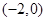 ,
,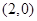 .直线
.直线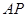 ,
,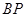 相交于点
相交于点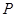 ,且它们的斜率之积是
,且它们的斜率之积是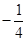 ,记动点
,记动点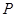 的轨迹为曲线
的轨迹为曲线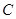 .
.
(1)求曲线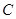 的方程;
的方程;
(2)设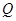 是曲线
是曲线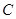 上的动点,直线
上的动点,直线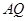 ,
,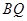 分别交直线
分别交直线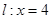 于点
于点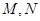 ,线段
,线段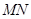 的中点为
的中点为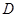 ,求直线
,求直线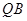 与直线
与直线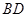 的斜率之积的取值范围;
的斜率之积的取值范围;
(3)在(2)的条件下,记直线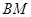 与
与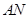 的交点为
的交点为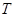 ,试探究点
,试探究点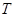 与曲线
与曲线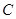 的位置关系,并说明理由.
的位置关系,并说明理由.
(本小题13分)已知抛物线的顶点在坐标原点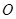 ,焦点
,焦点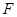 在
在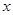 轴上,抛物线上的点
轴上,抛物线上的点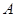 到
到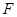 的距离为2,且
的距离为2,且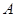 的横坐标为1.直线
的横坐标为1.直线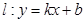 与抛物线交于
与抛物线交于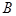 ,
,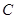 两点.
两点.
(1)求抛物线的方程;
(2)当直线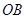 ,
,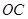 的倾斜角之和为
的倾斜角之和为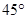 时,证明直线
时,证明直线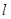 过定点.
过定点.
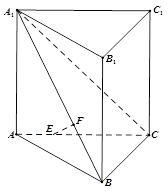
如图,在直三棱柱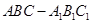 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面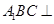 侧面
侧面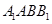 ,
,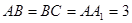 ,
,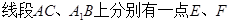 ,且满足
,且满足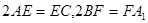 .
.
(1)求证: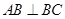 ;
;
(2)求点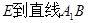 的距离;
的距离;
(3)求二面角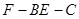 的平面角的余弦值.
的平面角的余弦值.
(本小题12分)已知命题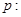 “存在
“存在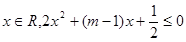 ”,命题
”,命题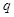 :“曲线
:“曲线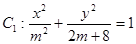 表示焦点在
表示焦点在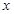 轴上的椭圆”,命题
轴上的椭圆”,命题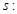 “曲线
“曲线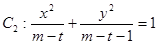 表示双曲线”
表示双曲线”
(1)若“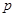 且
且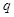 ”是真命题,求
”是真命题,求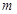 的取值范围;
的取值范围;
(2)若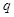 是
是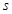 的必要不充分条件,求
的必要不充分条件,求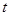 的取值范围。
的取值范围。
(本小题7分)已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=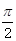 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).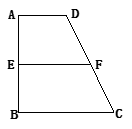
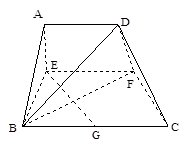
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;