(本小题满分10分)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3与x轴交于点A(﹣2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.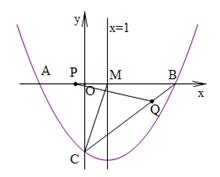
(1)求抛物线的解析式;
(2)动点P从点A出发沿线段AB以每秒3个单位长度的速度向点B运动,同时动点Q从点B出发沿线段BC以每秒2个单位长度的速度向点C运动,其中一个点到达终点时,另一个点也停止运动.设运动时间为t(秒),当以B、P、Q为顶点的三角形与△BCM相似时,求t的值;
(3)设点E在抛物线上,点F在对称轴上,在(2)的条件下,当点运动停止时,是否存在点E、F,使得以B、Q、E、F为顶点的四边形是平行四边形,如果存在写出点E的坐标,如果不存在,请说明理由.
南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:
| 运输工具 |
途中速度(km/h) |
途中费用(元/km) |
装卸费用(元) |
装卸时间 |
| 飞机 |
200 |
16 |
1000 |
2 |
| 火车 |
100 |
4 |
2000 |
4 |
| 汽车 |
50 |
8 |
1000 |
2 |
若这批水果在运输(包括装卸)过程中的损耗为200元/h,记A、B两市间的距离为xkm.
(1)如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求W1、W2、W3与x间的关系式;
(2)当x=250时,应采用哪种运输方式,才使运输时的总支出费用最小?
一个梯形,它的下底比上底长2cm,它的高为3cm,设它的上底长为xcm,它的面积为ycm2.
(1)写出y与x之间的关系式,并指出哪个变量是自变量,哪个变量是因变量.
(2)当x由5变7时,y如何变化?
(3)用表格表示当x从3变到10时(每次增加1),y的相应值.
(4)当x每增加1时,y如何变化?说明你的理由.
(5)这个梯形的面积能等于9cm2吗?能等于2cm2吗?为什么?
某单位为了丰富职工的业余文化生活,决定在广场放映露天电影,小明和小强吃过晚饭手拉手来到广场,准备看电影,可小明非要在背面看,于是小强在正面,小明在背面,如图,如果他俩眼睛在同一水平面上,而且看同一点时视线与水平线夹角相等.利用三角形全等,能判断他俩距屏幕一样远吗?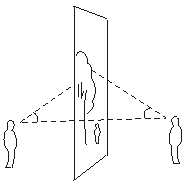
思考:结果为:___________.
证明:如图: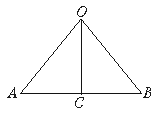
∠OAC=∠OBC
∵OC⊥AB
∴∠ACO=______=90°
在△OAC和△OBC中:
∠OAC=∠OBC
∠ACO=______
OC=______
∴△OAC≌△OBC,理由().
因此判断他们距屏幕的距离_________.
如图,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?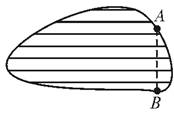
图是用10根火柴棒搭成的一个三角形,你能否移动其中的3根,摆出一对全等的三角形?画出你的修改方案.移动其中4根能否摆出一对全等三角形?请画图说明,并与同伴交流.