(本小题满分12分)(解答过程写在试卷上无效)
已知函数 ,
,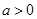 .
.
(1)若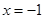 为
为 的极值点,求
的极值点,求 的单调区间;
的单调区间;
(2)如果对于一切 ,
, ,
,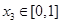 ,总存在以
,总存在以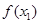 ,
,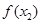 ,
,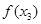 为三边长的三角形,试求实数
为三边长的三角形,试求实数 的取值范围.
的取值范围.
设函数 ,
,
 .
.
⑴ 求不等式 的解集;
的解集;
⑵ 如果关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
,
以原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
⑴ 求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
⑵ 当 时,曲线
时,曲线 和
和 相交于
相交于 、
、 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.
如图, 是
是 的直径,弦
的直径,弦 与
与 垂直,并与
垂直,并与 相交于点
相交于点 ,点
,点 为弦
为弦 上异于点
上异于点 的任意一点,连结
的任意一点,连结 、
、 并延长交
并延长交 于点
于点 、
、 .
.
⑴ 求证: 、
、 、
、 、
、 四点共圆;
四点共圆;
⑵ 求证: .
.
已知函数 .
.
⑴ 求函数 的单调区间;
的单调区间;
⑵ 如果对于任意的 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
⑶ 设函数 ,
, . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列 ,求数列
,求数列 的所有项之和
的所有项之和 的值.
的值.
如图,曲线 与曲线
与曲线 相交于
相交于 、
、 、
、 、
、 四个点.
四个点.
⑴ 求 的取值范围;
的取值范围;
⑵ 求四边形 的面积的最大值及此时对角线
的面积的最大值及此时对角线 与
与 的交点坐标.
的交点坐标.