(本小题满分10分)选修4—1:几何证明选讲
如图,在 直径
直径 的延长线上任取一点
的延长线上任取一点 ,过点
,过点 做直线
做直线 与
与 交于点
交于点 、
、 ,在
,在 上取一点
上取一点 ,使
,使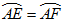 ,连接
,连接 ,交
,交 于
于 .
.
(1)求证: 、
、 、
、 、
、 四点共圆;
四点共圆;
(2)若 ,求
,求 的值.
的值.
在△ABC中,角A,B,C所对的边分别是a,b,c.己知csin A=  acos C.
acos C.
(I)求C;
(II)若c=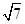 ,且
,且 求△ABC的面积.
求△ABC的面积.
已知等差数列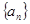 的前
的前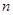 项和为
项和为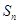 ,
,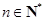 ,且
,且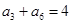 ,
,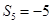 .
.
(Ⅰ)求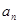 ;
;
(Ⅱ)若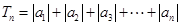 ,求
,求 的值和
的值和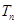 的表达式
的表达式
已知椭圆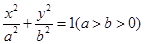 的离心率为
的离心率为 ,其左焦点
,其左焦点 到点
到点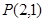 的距离为
的距离为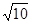 .
.
(1)求椭圆的方程;
(2)过右焦点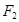 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点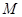 、
、 ,则
,则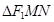 内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
已知数列 ,
,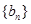 满足
满足 ,
,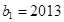 ,且对任意的正整数
,且对任意的正整数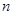 ,
, 和
和 均成等比数列.
均成等比数列.
(1)求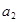 、
、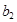 的值;
的值;
(2)证明: 和
和 均成等比数列;
均成等比数列;
(3)是否存在唯一正整数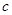 ,使得
,使得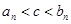 恒成立?证明你的结论.
恒成立?证明你的结论.
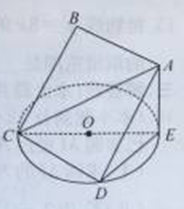
如图,正方形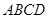 所在平面与圆
所在平面与圆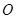 所在的平面相交于
所在的平面相交于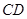 ,线段
,线段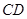 为圆
为圆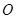 的弦,
的弦,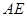 垂直于圆
垂直于圆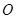 所在的平面,垂足
所在的平面,垂足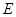 为圆
为圆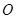 上异于
上异于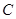 、
、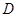 的点,设正方形
的点,设正方形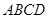 的边长为
的边长为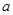 ,且
,且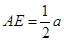 .
.
(1)求证:平面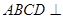 平面
平面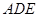 ;
;
(2)若异面直线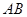 与
与 所成的角为
所成的角为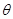 ,
,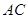 与底面
与底面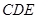 所成角为
所成角为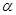 ,二面角
,二面角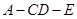 所成角为
所成角为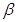 ,求证
,求证