（本题8分）在一次数学课上，老师在屏幕上出示了一个例题：在△ABC中，D，E分别是AB，AC上的一点，BE与CD交于点O，画出图形（如图），给出下列四个条件：①∠DBO=∠ECO；②∠BDO=∠CEO；③BD=CE；④OB=OC．
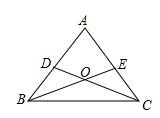
（1）要求同学从这四个等式中选出两个作为已知条件，可判定△ABC是等腰三角形．
请你用序号在横线上写出所有情形．答：
（2）选择第（1）题中的一种情形，说明△ABC是等腰三角形的理由，并写出解题过程．
解：我选择 ．
证明：
●探究 (1) 在图1中，已知线段AB，CD，其中点分别为E，F．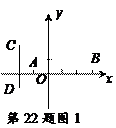
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
(2)在图2中，已知线段AB的端点坐标为A(a，b) ，B(c，d)，求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．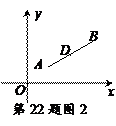
●归纳无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A(a，b)，B(c，d)， AB中点为D(x，y) 时，x=_________，y=___________．（不必证明）
●运用在图3中，一次函数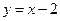
与反比例函数
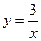的图象交点为A，B．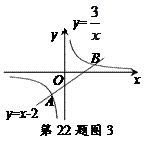
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．
为迎接第四届世界太阳城大会，德州市把主要路段路灯更换为太阳能路灯．已知太阳能路灯售价为5000元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过100个，按原价付款；若一次购买100个以上，且购买的个数每增加一个，其价格减少10元，但太阳能路灯的售价不得低于3500元/个．乙店一律按原价的80℅销售．现购买太阳能路灯x个，如果全部在甲商家购买，则所需金额为y1元；如果全部在乙商家购买，则所需金额为y2元.
（1）分别求出y1、y2与x之间的函数关系式；
（2）若市政府投资140万元，最多能购买多少个太阳能路灯？
如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点, 交AD于点G，交AB于点F．
（1）求证：BC与⊙O相切；
（2）当∠BAC=120°时，求∠EFG的度数．
某工厂甲、乙两名工人参加操作技能培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：
| 甲 |
95 |
82 |
88 |
81 |
93 |
79 |
84 |
78 |
| 乙 |
83 |
92 |
80 |
95 |
90 |
80 |
85 |
75 |
(1)请你计算这两组数据的平均数、中位数；
(2)现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．
如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．
(1)求证：AB＝DC；
(2)试判断△OEF的形状，并说明理由．