( 本小题满分12分)已知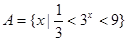 ,
,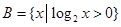 .
.
(1)求 和
和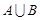 ;
;
(2)定义 且
且 ,求
,求 和
和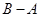 .
.
定义在R上的单调函数f(x)满足f(3)=log23且对任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求证f(x)为奇函数;
(2)若f(k·3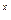 )+f(3
)+f(3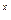 -9
-9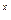 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米
(1)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(2)当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值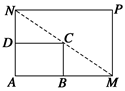
已知函数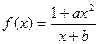
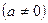 是奇函数,并且函数
是奇函数,并且函数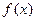 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数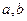 的值;(2)求函数
的值;(2)求函数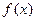 的值域
的值域
已知函数 .
.
(1)若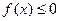 的解集为
的解集为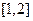 ,求实数
,求实数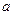 的值;
的值;
(2)在(1)的条件下,求函数f(x)在区间[0,3]的值域.
(本小题满分16分)
已知函数 (
( 是自然对数的底数).
是自然对数的底数).
(1)若曲线 在
在 处的切线也是抛物线
处的切线也是抛物线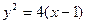 的切线,求
的切线,求 的值;
的值;
(2)若对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)当 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点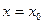 处的切线斜率与
处的切线斜率与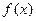 在
在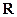 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.