(本小题满分10分)选修4-5不等式选讲
已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集.
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
(本小题满分14分)已知函数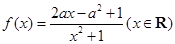 ,其中
,其中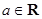 .
.
(Ⅰ)当 时,求曲线
时,求曲线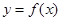 在点
在点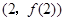 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
(本小题满分14分)已知圆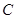 过点
过点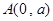
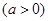 , 且在
, 且在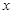 轴上截得的弦
轴上截得的弦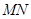 的长为
的长为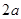 .
.
(1) 求圆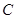 的圆心的轨迹方程;
的圆心的轨迹方程;
(2) 若 , 求圆
, 求圆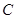 的方程.
的方程.
(本小题满分14分)设数列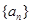 的前
的前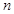 项和为
项和为 ,点
,点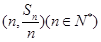 均在函数
均在函数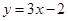 的图像上.
的图像上.
(Ⅰ)求数列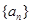 的通项公式;
的通项公式;
(Ⅱ)设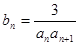 ,
, 是数列
是数列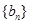 的前
的前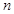 项和,求使得
项和,求使得 对所有
对所有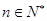 都成立的最小正整数
都成立的最小正整数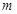 .
.
(本小题满分13分)如图,正方形 所在平面与三角形
所在平面与三角形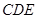 所在平面相交于
所在平面相交于 ,
,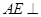 平面
平面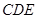 ,且
,且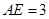 ,
,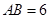
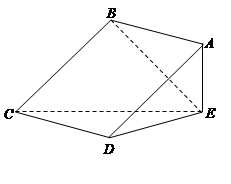
(1)求证: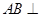 平面
平面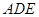 ;
;
(2)求凸多面体 的体积.
的体积.
(本小题满分13分)
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:
(Ⅰ)连续取两次都是白球的概率;
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.