(本小题满分10分)选修4-1:几何证明选讲
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x方程x2-14x+mn=0的两个根.
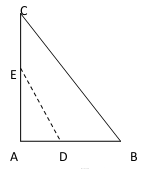
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
已知函数f(x)=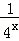 ﹣
﹣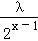 +3(﹣1≤x≤2).
+3(﹣1≤x≤2).
(1)若λ=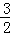 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若函数f(x)的最小值是1,求实数λ的值.
函数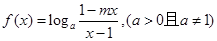 是奇函数.
是奇函数.
(1)求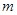 的值;
的值;
(2)判断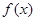 在区间
在区间 上单调性并加以证明;
上单调性并加以证明;
设二次函数f(x)=ax2+bx+c的图象过点(0,1)和(1,4),且对于任意的实数x,不等式f(x)≥4x恒成立.
(1)求函数f(x)的表达式;
(2)设g(x)=kx+1,若G(x)= 在区间[1,2]上是增函数,求实数k的取值范围。
在区间[1,2]上是增函数,求实数k的取值范围。
设函数f(x)=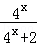 ,则:
,则:
(1)证明:f(x)+f(1﹣x)=1;
(2)计算:f( )+f(
)+f(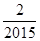 )+f(
)+f( )+…+f(
)+…+f(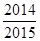 ).
).
(1)计算:
 +lg25+lg4+
+lg25+lg4+ +
+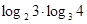 ;
;
(2)设集合A={x|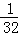 ≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.
≤2﹣x≤4},B={x|m﹣1<x<2m+1}.若A∪B=A,求m的取值范围.