(本小题满分13分)
甲、乙两人进行五局三胜制的游戏(即先胜三局者获胜),若甲每局胜率为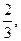 乙每局胜率为
乙每局胜率为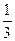 ,设每局比赛之间相互没有影响。
,设每局比赛之间相互没有影响。
(1)恰好第五局甲胜的概率;
(2)记ξ为本次游戏的局数,求ξ的概率分布列和数学期望。
下表是某小卖部6天卖出热茶的杯数与当天气温的对比表:
| 气温/℃ |
26 |
18 |
13 |
10 |
4 |
-1 |
| 杯数 |
20 |
24 |
34 |
38 |
50 |
64 |
(1)将上表中的数据制成散点图.
(2)你能从散点图中发现温度与饮料杯数近似成什么关系吗?
(3)如果近似成线性关系的话,请求出回归直线方程来近似地表示这种线性关系.
(4)如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
为了让学生了解更多“社会法律”知识,
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
某中学举行了一次“社会法律知识竞赛”,
共有800名学生参加了这次竞赛. 为了解
本次竞赛成绩情况,从中抽取了部分学
生的成绩(得分均为整数,满分为100
分)进行统计.请你根据尚未完成并有
局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,
现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格1 2 3 4 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人?
记集合 ,
,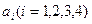 是
是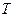 中可重复选取的元素.
中可重复选取的元素.
(1)若将集合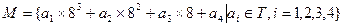 中所有元素按从小到大的顺序排列,求第2008个数所对应的
中所有元素按从小到大的顺序排列,求第2008个数所对应的 的值;
的值;
(2)若将集合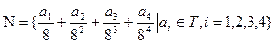 中所有元素按从大到小的顺序排列,求第2008个数所对应的
中所有元素按从大到小的顺序排列,求第2008个数所对应的 的值.
的值.