(本小题满分12分)甲、乙两袋中各装有大小相同的小球 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为 、
、 、
、 ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为 ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)
甲乙二人用4张扑克牌(分别是红桃2, 红桃3, 红桃4, 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(Ⅰ)设 分别表示甲、乙抽到的牌的数字
分别表示甲、乙抽到的牌的数字 ,写出甲乙二人抽到的牌的所有情况.
,写出甲乙二人抽到的牌的所有情况.
(Ⅱ)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜.你认为此游戏是否公平,说明你的理由.
(本小题满分14分)
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱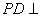 底面ABCD,
底面ABCD,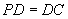 ,E是PC的中点,作
,E是PC的中点,作 交PB于点F;
交PB于点F;
(I)证明  平面
平面 ;
;
(II)证明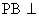 平面EFD;
平面EFD;
(本小题满分12分)已知 定义域为R,
定义域为R,
(1)求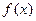 的值域;
的值域;
(2在区间 上,
上,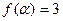 ,求
,求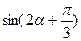 )
)
已知
 .
.
(1)当 时,求
时,求 上的值域;
上的值域;
(2) 求函数 在
在 上的最小值;
上的最小值;
(3) 证明: 对一切 ,都有
,都有 成立
成立
已知函数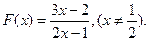
(1)求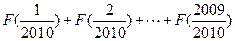 的值;
的值;
(2)已知数列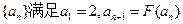 ,求证数列
,求证数列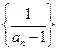 是等差数列;
是等差数列;
(3)已知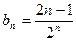 ,求数列
,求数列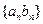 的前n项和
的前n项和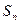 .
.