(本题12分)已知定义在区间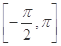 上的函数
上的函数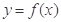 的图像关于直线
的图像关于直线 对称,当
对称,当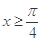 时,函数
时,函数 .
.
(1)求 的值;
的值;
(2)求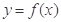 的表达式;
的表达式;
(3)若关于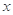 的方程
的方程 有解,那么将方程在
有解,那么将方程在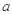 取某一确定值时所求得的所有解的和记为
取某一确定值时所求得的所有解的和记为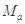 ,求
,求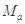 的所有可能取值及相应
的所有可能取值及相应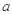 的的取值范围.
的的取值范围.
若双曲线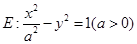 的离心率等于
的离心率等于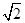 ,直线
,直线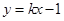 与双曲线
与双曲线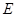 的右支交于
的右支交于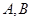 两点.
两点.
(1)求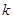 的取值范围;
的取值范围;
(2)若 ,点
,点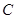 是双曲线
是双曲线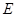 上一点,且
上一点,且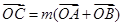 ,求
,求
设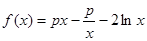 .
.
(Ⅰ)若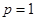 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)设 ,且
,且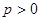 ,若在
,若在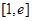 上至少存在一点
上至少存在一点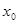 ,使得
,使得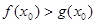 成立,求实数p的取值范围.
成立,求实数p的取值范围.
某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对 表示“甲在
表示“甲在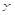 号车站下车,乙在
号车站下车,乙在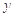 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
如图(1)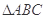 是等腰直角三角形,其中
是等腰直角三角形,其中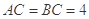 ,
,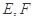 分别为
分别为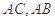 的中点,将
的中点,将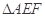 沿
沿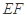 折起,点
折起,点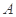 的位置变为点
的位置变为点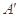 ,已知点
,已知点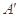 在平面
在平面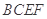 上的射影
上的射影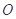 为
为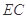 的中点,如图(2)所示.
的中点,如图(2)所示.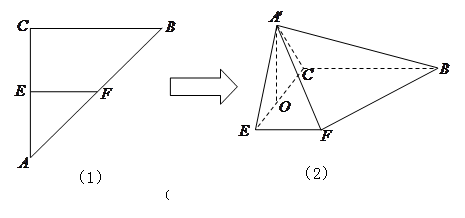
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥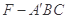 的体积.
的体积.
在各项均为负数的数列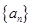 中,已知点
中,已知点
 在函数
在函数 的图像上,且
的图像上,且 .
.
(Ⅰ)求数列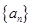 的通项公式;
的通项公式;
(Ⅱ)若数列 的前n项和为
的前n项和为 ,且
,且 ,求
,求