(本小题满分12分)已知非零向量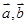 满足
满足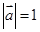 ,且
,且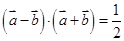 .
.
(1)求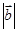 ;
;
(2)当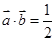 时,求向量
时,求向量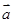 与
与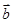 的夹角的值.
的夹角的值.
(本小题14分)如图,三棱锥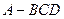 中,
中,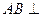 平面
平面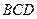 ,
, ,
,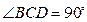 ,
, 分别是
分别是 上
上
的动点,且 平面
平面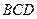 ,二面角
,二面角 为
为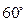 .
.
(1)求证: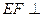 平面
平面 ;
;
(2)若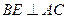 ,求直线
,求直线 与平面
与平面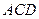 所成角的余弦值.
所成角的余弦值.
(本小题14分)数 列
列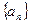 中,
中, ,
, (k≠0)对任意
(k≠0)对任意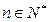 成立,令
成立,令 ,且
,且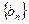 是等比数列.
是等比数列. (1)求实数
(1)求实数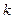 的值;(2)求数列
的值;(2)求数列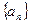 的通项公式.
的通项公式.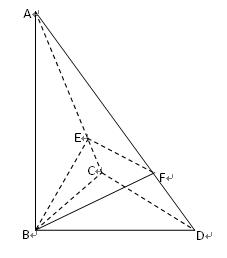
(本小题14分)已知 中,
中, 的对边分别为
的对边分别为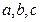 ,且
,且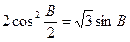 ,
, 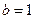 .(1)若
.(1)若 ,求边
,求边 的大小;(2)求
的大小;(2)求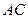 边上高的最大值.
边上高的最大值.
(本小题满分12分)
如图,在棱长为1的正方体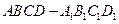 中,
中, 是侧棱
是侧棱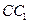 上的一点,
上的一点, .
.
(1)试确定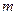 ,使直线
,使直线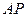 与平面
与平面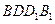
所成角的正切值为 ;
;
(2)在线段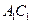 上是否存在一个定点
上是否存在一个定点 ,
,
使得对任意的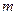 ,
,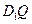 在平面
在平面 上
上
的射影垂直于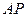 ,并证明你的结论.
,并证明你的结论.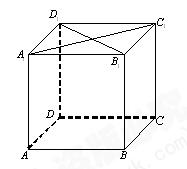
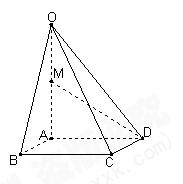
(本小题满分12分)
如图,在四棱锥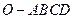 中,底面
中,底面 四边长为1的
四边长为1的
菱形,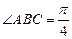 ,
,  ,
, 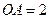 ,
, 为
为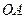 的中点.
的中点.
(Ⅰ)求异面直线AB与MD所成角的大小 ;
;
(Ⅱ)求点B到平面OCD的距离.