（本小题满分12分）通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
性别与看营养说明列联表 单位 名
| |
男 |
女 |
总计 |
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
（1）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为10的样本，问样本中看与不看营养说明的女生各有多少名?
（2）根据以上列联表，能否在犯错误的概率不超过0．01的前提下认为性别与是否看营养说明之间有关系？
下面的临界值表供参考：
 |
0．15 |
0．10 |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
 |
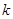2．072 |
2．706 |
3．841 |
5．024 |
6．635 |
7．879 |
10．828 |
（参考公式：
，其中
）
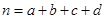（本小题满分13分）已知函数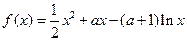
（
）．
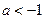（1）若函数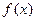
在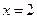
处的切线与x轴平行，求a的值，并求出函数的极值；
（2）已知函数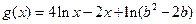
，在（1）的条件下，若
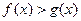恒成立，求b的取值范围．
（本小题满分12分）
设数列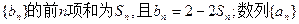
为等差数列，且a5=14，a7=20。
（1）求数列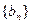
的通项公式；
（2）若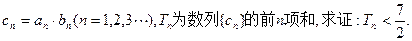
已知直线l经过抛物线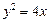
的焦点F，
且与抛物线相交于A、B两点.
（1）若
，求点A的坐标；
（2）若直线l的倾斜角为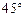
，求线段AB的长.
.(本小题满分12分)
在△ABC中，角A、B、C的对应边分别为a，b，c，且满足a2－ab＋b2＝c2.
(1)求角C；
(2)若△ABC的面积为，c＝2，求a＋b的值.
：已知矩阵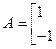
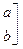,A的一个特征值
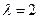，其对应的特征向量是
.
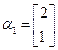（Ⅰ）求矩阵
；
（Ⅱ）求直线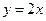
在矩阵M所对应的线性变换下的像的方程