已知,如图,E在△ABC的边AC上,且∠AEB=∠ABC.
(1)求证:∠ABE=∠C
(2)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.
如图,已知CD是Rt△ABC斜边上的高,AC=4,BC=3,计算cos∠BCD的值.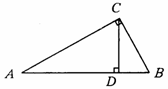
如图,已知⊙O的半径为5,弦AB=8,OC⊥AB于C,求OC的长.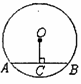
如图,OABC是一个放在平面直角坐标系中的矩形,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=3,OC=4,平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线运动的时间为t(秒).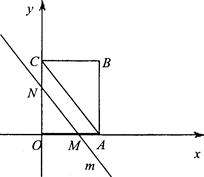
(1)写出点B的坐标;
(2)t为何值时,MN=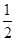 AC;
AC;
(3)设△OMN的面积为S,求S与t的函数关系式,并写出t的取值范围;当t为何值时,S有最大值?并求S的最大值.
如图,抛物线y=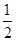 x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.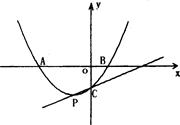
(1)求m、n的值;
(2)求直线PC的解析式;
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系,并说明理由.(参考数据: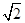 ≈1.41,
≈1.41,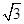 ≈1.73,
≈1.73,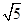 ≈2.24)
≈2.24)
如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,sin∠AOB=,反比例函数y=(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.