数学活动——“关于三角形全等的条件”
1.【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
2.【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
3.【逐步探究】
(1)第一种情况:当∠B是直角时,如图①,根据______定理,可得△ABC≌△DEF.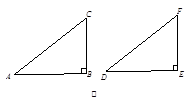
(2)第二种情况:当∠B是钝角时,△ABC≌△DEF仍成立.请你完成证明.
已知:如图②,△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,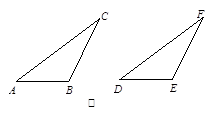
求证:△ABC≌△DEF.
证明:
(3)第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)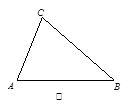
(4)【深入思考】
∠B还要满足什么条件,就可以使△ABC≌△DEF?(请直接写出结论.)
在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若∠B _________,则△ABC≌△DEF.
已知,如图,一次函数 、 为常数, 的图象与 轴、 轴分别交于 、 两点,且与反比例函数 为常数且 的图象在第二象限交于点 . 轴,垂足为 ,若 .
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式: 的解集.

如图,在平面直角坐标系 中,以点 为圆心的圆分别交 轴的正半轴于点 ,交 轴的正半轴于点 .劣弧 的长为 ,直线 与 轴、 轴分别交于点 、 .
(1)求证:直线 与 相切;
(2)求图中所示的阴影部分的面积(结果用 表示)
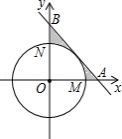
随着国家“惠民政策”的陆续出台,为了切实让老百姓得到实惠,国家卫计委通过严打药品销售环节中的不正当行为,某种药品原价200元 瓶,经过连续两次降价后,现在仅卖98元 瓶,现假定两次降价的百分率相同,求该种药品平均每次降价的百分率.
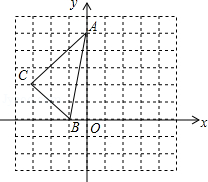
如图,方格中,每个小正方形的边长都是单位1, 在平面直角坐标系中的位置如图.
(1)画出将 向右平移2个单位得到△ ;
(2)画出将 绕点 顺时针方向旋转 得到的△ ;
(3)求△ 与△ 重合部分的面积.
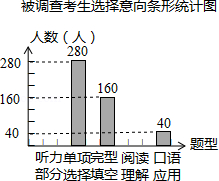
为了解中考考生最喜欢做哪种类型的英语客观题,2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查,要求每位考生都自主选择其中一个类型,为此随机调查了各考点部分考生的意向.并将调查结果绘制成如图的统计图表(问卷回收率为 ,并均为有效问卷).
被调查考生选择意向统计表
|
题型 |
所占百分比 |
|
听力部分 |
|
|
单项选择 |
|
|
完型填空 |
|
|
阅读理解 |
|
|
口语应用 |
|
根据统计图表中的信息,解答下列问题:
(1)求本次被调查的考生总人数及 、 、 的值;
(2)将条形统计图补充完整;
(3)全市参加这次中考的考生共有42000人,试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人?