A，B分别为数轴上的两点，点A对应的数为﹣20，点B对应的数为100．
（1）请写出与A，B两点距离相等的点M所对应的数；
（2）现有一只电子蚂蚁P从B出发，以6单位/秒速度向左移动，同时另一只电子蚂蚁Q恰好从A点出发，以4单位/秒速度向右运动，设两只电子蚂蚁在C相遇，你知道点C对应的数是多少吗？
（年广西来宾10分）如图，AB为⊙O的直径，BF切⊙O于点B，AF交⊙O于点D，点C在DF上，BC交⊙O于点E，且∠BAF=2∠CBF，CG⊥BF于点G，连接AE．
（1）直接写出AE与BC的位置关系；
（2）求证：△BCG∽△ACE；
（3）若∠F=60°，GF=1，求⊙O的半径长．
（年广东深圳9分）如图，在平面直角坐标系中，⊙M过原点O，与x轴交于A（4，0），与y轴交于B（0，3），点C为劣弧AO的中点，连接AC并延长到D，使DC=4CA，连接BD．
（1）求⊙M的半径；
（2）证明：BD为⊙M的切线；
（3）在直线MC上找一点P，使|DP﹣AP|最大．
（年广东汕尾11分）如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于E．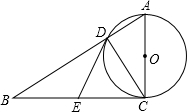
（1）求证：点E是边BC的中点；
（2）求证：BC2=BD•BA；
（3）当以点O、D、E、C为顶点的四边形是正方形时，求证：△ABC是等腰直角三角形．
（2013年四川宜宾3分）如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足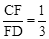
，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=
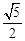；④S△DEF=4
．
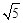其中正确的是 （写出所有正确结论的序号）．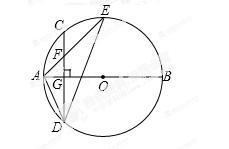
（年广西桂林10分）如图，△ABC的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD于E，交AB于F，交⊙O于G。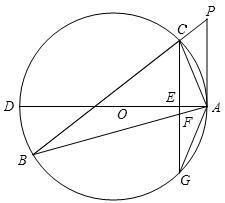
（1）判断直线PA与⊙O的位置关系，并说明理由；
（2）求证：AG2=AF·AB；
（3）求若⊙O的直径为10，AC=2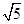
，AB=4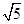，求△AFG的面积.