（本题9分）如图，
点
在
轴的正半轴上，
，
，
．点
从点
出发，沿
轴向左以每秒1个单位长的速度运动，运动时间为
秒．
（1）点的坐标是 ；
（2）当
时，求的值；
（3）以点为圆心，
为半径的
随点的运动而变化，当与四边形
的边（或边所在的直线）相切时，求的值．
因式分解（本题6分）
（1）
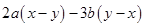
（2）（a-3）2-6（a-3）+9
计算（本题9分）
（1）
（2）
（3）
体育课上，全班男同学进行了100米测验，达标成绩为15秒，下表是某小组８名男生的成绩斐然记录，其中＂＋＂表示成绩大于15秒．
| －0．8 |
+1 |
－1．2 |
0 |
－0．7 |
＋0．6 |
－0．4 |
－0．1 |
问：（1）这个小组男生的达标率为多少？（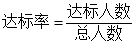
）
（2）这个小组男生的平均成绩是多少秒？
画一条数轴，并在数轴上表示：3．5和它的相反数，－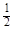
和它的倒数，绝对值等于3的数，最大的负整数和它的平方，并把这些数由小到大用“<”号连接起来。
下表列出了国外几个城市与北京的时差（带正号的数表示同一时刻比北京的时间早的时数）。现在的北京时间是上午8∶00
（1）求现在纽约时间是多少？
（2）斌斌现在想给远在巴黎的姑妈打电话，你认为合适吗？
| 城市 |
时差/ 时 |
| 纽约 |
－13 |
| 巴黎 |
－7 |
| 东京 |
＋1 |
| 芝 加 哥 |
－14 |