(1)已知a>b>0,c<d<0,e<0,比较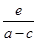 与
与 的大小.
的大小.
(2)已知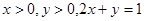 ,求
,求 的范围
的范围
如图,在四棱锥 中,底面 是平行四边形, ,M,N分别为 的中点, .

(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
设函数 .
(1)求函数 的最小正周期;
(2)求函数 在 上的最大值.
已知函数 .
(1)讨论 的单调性;
(2)从下面两个条件中选一个,证明: 有一个零点
① ;
② .
一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代……,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数, .
(1)已知 ,求 ;
(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程: 的一个最小正实根,求证:当 时, ,当 时, ;
(3)根据你的理解说明(2)问结论的实际含义.
已知椭圆C的方程为 ,右焦点为 ,且离心率为 .
(1)求椭圆C的方程;
(2)设M,N是椭圆C上的两点,直线 与曲线 相切.证明:M,N,F三点共线的充要条件是 .