(
已知三个函数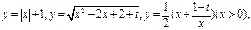 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的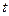 为同一个常数,且
为同一个常数,且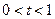 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程 的三个根.
的三个根.
(Ⅰ) 求证: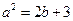 ;
;
(Ⅱ) 设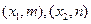 是函数
是函数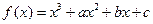 的两个极值点,求
的两个极值点,求 的取值范围.
的取值范围.
如图,已知直线 (
( )与抛物线
)与抛物线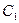 :
: 和圆
和圆 :
: 都相切,
都相切, 是
是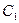 的焦点.
的焦点.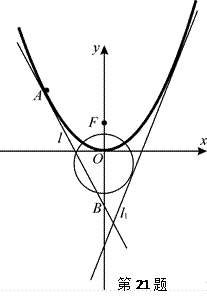
(Ⅰ)求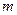 与
与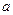 的值;
的值;
(Ⅱ)设 是
是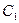 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线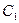 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点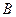 ,以
,以 、
、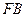 为邻边作平行四边形
为邻边作平行四边形 ,证明:点
,证明:点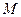 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点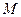 所在的定直线为
所在的定直线为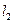 ,直线
,直线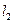 与
与 轴交点为
轴交点为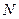 ,连接
,连接 交抛物线
交抛物线 于
于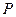 、
、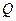 两点,求△
两点,求△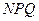 的面积
的面积 的取值范围.
的取值范围.
(
已知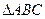 与
与 都是边长为2的等边三角形,且平面
都是边长为2的等边三角形,且平面 平面
平面 ,过点
,过点 作
作 平面
平面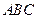 ,且
,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小.
所成角的大小.
等差数列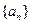 中,
中, ,前
,前 项和为
项和为 ,等比数列
,等比数列 各项均为正数,
各项均为正数,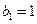 ,且
,且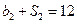 ,
, 的公比
的公比 .
.
(Ⅰ)求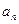 与
与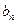 ;
;
(Ⅱ)设 ,求数列
,求数列 的前项和
的前项和 .
.
已知函数 .
.
(Ⅰ)求 的值域;
的值域;
(Ⅱ)设 的角
的角 的对边分别为
的对边分别为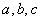 ,且
,且 求
求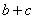 的取值范围.
的取值范围.