(本小题满分12分)在三棱锥M-ABC中,AB=2AC=2,MA=MB= ,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
(1)证明:CM^SN;
(2)求SN与平面CMN所成角的大小.
某次数学考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(I)从两班10名同学中各抽取一人,已知有人及格,求乙班同学不及格的概率;
(II)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为X,求X的分布列和期望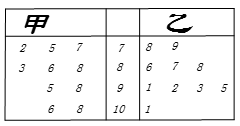
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB= ,点E是棱PB的中点.
,点E是棱PB的中点.
(Ⅰ) 求直线AD与平面PBC的距离;
(Ⅱ) 若AD= ,求二面角A-EC-D的平面角的余弦值.
,求二面角A-EC-D的平面角的余弦值.
已知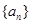 是一个等差数列,且
是一个等差数列,且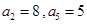 .等比数列
.等比数列 的前
的前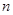 项和为
项和为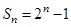 .
.
(I)求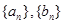 的通项公式;
的通项公式;
(II)求数列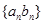 的最大项及相应
的最大项及相应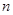 的值.
的值.
设函数 其中
其中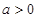 ,
,
(1)求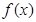 的单调区间;
的单调区间;
(2)当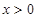 时,证明不等式:
时,证明不等式: .
.
(3)求证:ln(n+1)> 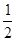 +
+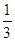 +
+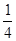 +L
+L (
(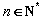 ).
).
已知数列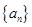 中,
中,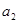 =
= (
(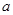 为常数);
为常数);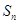 是
是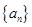 的前
的前 项和,且
项和,且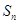 是
是 与
与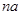 的等差中项。
的等差中项。
(1)求 ;
;
(2)猜想 的表达式,并用数学归纳法加以证明;
的表达式,并用数学归纳法加以证明;
(3)求证以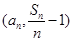 为坐标的点
为坐标的点 都落在同一直线上。
都落在同一直线上。