如图所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到五棱锥P﹣ABFED,且 ,PB=
,PB= .
.
(1)求证:BD⊥平面POA;
(2)求二面角B﹣AP﹣O的正切值.
记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
=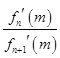 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
设f(x)是定义在区间(1,+∞)上的函数,其导函数为f′(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数f(x)=ln x+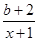 (x>1),其中b为实数.
(x>1),其中b为实数.
①求证:函数f(x)具有性质P(b);
②求函数f(x)的单调区间;
(2)已知函数g(x)具有性质P(2).给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范围.
已知函数f(x)=ax2+1,g(x)=x3+bx,其中a>0,b>0.
(1)若曲线y=f(x)与曲线y=g(x) 在它们的交点P(2,c)处有相同的切线(P为切点),求实数a,b的值;
(2)令h (x)=f(x)+g(x),若函数h(x)的单调减区间为 .
.
①求函数h(x)在区间(-∞,-1]上的最大值M(a);
②若|h(x)|≤3在x∈[-2,0]上恒成立,求实数a的取值范围.
已知函数f(x)=ax+x2-xln a(a>0,a≠1).
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调增区间;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1 m的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轮迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:m.
(1)求助跑道所在的抛物线方程;
(2)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4 m到6 m之间(包括4 m和6 m),试求运动员飞行过程中距离平台最大高度的取值范围.
(注:飞行距离指点C与点E的水平距离,即这两点横坐标差的绝对值)