(本小题满分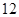 分)为考察高中生的性别与是否喜欢体育课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下
分)为考察高中生的性别与是否喜欢体育课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下 列联表:
列联表:
| |
喜欢体育课 |
不喜欢体育课 |
合计 |
| 男 |
30 |
60 |
90 |
| 女 |
20 |
90 |
110 |
| 合计 |
50 |
150 |
200 |
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢体育课之间有关系”?
(2)若采用分层抽样的方法从不喜欢体育课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为 ,求
,求 的数学期望.
的数学期望.
选修4—1:矩阵与变换
已知二阶矩阵A有特征值 及对应的一个特征向量
及对应的一个特征向量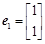 和特征值
和特征值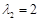 及对应
及对应
的一个特征向量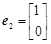 ,试求矩阵A.
,试求矩阵A.
.(本小题满分16分)
数列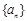 中,
中, ,
,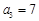 ,且
,且 .
.
(1)求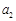 及
及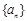 的通项公式;
的通项公式;
(2)设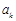 是
是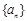 中的任意一项,是否存在
中的任意一项,是否存在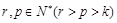 ,使
,使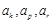 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出 和
和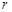 关于
关于 的一个表达式,并给出证明;
的一个表达式,并给出证明;
(3)证明:对一切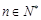 ,
,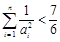 .
.
.(本小题满分16分)
函数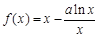 ,其中
,其中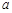 为常数.
为常数.
(1)证明:对任意 ,函数
,函数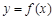 图像恒过定点;
图像恒过定点;
(2)当 时,不等式
时,不等式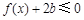 在
在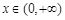 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若对任意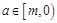 时,函数
时,函数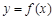 在定义域上恒单调递增,求
在定义域上恒单调递增,求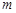 的最小值.
的最小值.
.(本小题满分16分)
已知椭圆
 上的一动点
上的一动点 到右焦点的最短距离为
到右焦点的最短距离为 ,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆
,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆 的方程;
的方程;
(2)设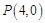 ,
,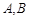 是椭圆
是椭圆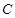 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结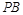 交椭圆
交椭圆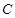 于另一点
于另一点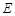 ,证明直线
,证明直线 与
与 轴相交于定点
轴相交于定点 ;
;
(3)在(2)的条件下,过点 的直线与椭圆
的直线与椭圆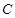 交于
交于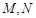 两点,求
两点,求 的取值
的取值
范围.
.(本小题满分14分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收
益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单
位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.现
有两个奖励方案的函数模型:(1)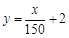 ;(2)
;(2)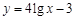 .试问这两个函数模
.试问这两个函数模
型是否符合该公司要求,并说明理由.