(本小题满分12分)
定义在R上的函数f(x)满足对任意的x,y∈R都有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0.
(1)求证:f(x)为奇函数;
(2)判断f(x)的单调性并证明;
(3)解不等式:f[log2(x+ +6)]+f(-3)≤0.
+6)]+f(-3)≤0.
若下列方程: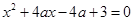 ,
,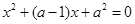 ,
,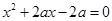 ,至少有一个方程有实根,试求实数
,至少有一个方程有实根,试求实数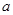 的取值范围.
的取值范围.
解:设三个方程均无实根,则有
解得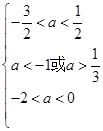 ,即
,即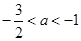 .
.
所以当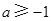 或
或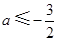 时,三个方程至少有一个方程有实根.
时,三个方程至少有一个方程有实根.
已知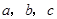 为互不相等的实数,求证:
为互不相等的实数,求证: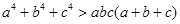 .
.
(本小题满分12分) 已知椭圆 的离心率
的离心率 ,A,B
,A,B
分别为椭圆的长轴和短轴的端点, 为AB的中点,O为坐标原点,且
为AB的中点,O为坐标原点,且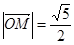 .
.
(1)求椭圆的方程;
(2)过(-1,0)的直线 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线 的方程.
的方程.
(本小题满分12分)双曲线 的离心率为2,坐标原点到
的离心率为2,坐标原点到
直线AB的距离为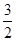 ,其中A
,其中A ,B
,B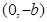 .
.
(1)求双曲线的方程;
(2)若 是双曲线虚轴在
是双曲线虚轴在 轴正半轴上的端点,过
轴正半轴上的端点,过 作直线与双曲线交于
作直线与双曲线交于 两点,求
两点,求 时,直线
时,直线 的方程.
的方程.
已知平面内一动点P到F(1,0)的距离比点P到 轴的距离少1.
轴的距离少1.
(1)求动点P的轨迹C的方程;
(2)过点F的直线交轨迹C于A,B两点,交直线 于
于 点,且
点,且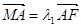 ,
,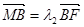 ,
,
求 的值。
的值。