(本小题满分12分)
已知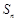 是数列
是数列 的前n项和,满足
的前n项和,满足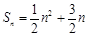 ,正项等比数列
,正项等比数列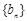 的前n项和为
的前n项和为 ,且满足
,且满足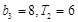 .
.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记 ,求数列{cn}的前n项和
,求数列{cn}的前n项和 .
.
(本小题满分14分)设点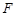 为椭圆
为椭圆 的右焦点,点
的右焦点,点 在椭圆
在椭圆 上,已知椭圆
上,已知椭圆 的离心率为
的离心率为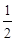 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过右焦点 的直线
的直线 与椭圆相交于
与椭圆相交于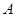 ,
, 两点,记
两点,记 三条边所在直线的斜率的乘积为
三条边所在直线的斜率的乘积为 ,求
,求 的最大值.
的最大值.
(本小题满分13分)2014年12月28日开始,北京市公共电汽车和地铁按照里程分段计价. 具体如下表.(不考虑公交卡折扣情况)
| 乘公共电汽车方案 |
10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含). |
乘坐地铁方案(不含机场线) |
6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含). |
已知在北京地铁四号线上,任意一站到陶然亭站的票价不超过5元,现从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.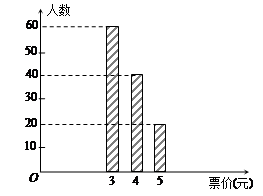
(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6人乘坐地铁的票价情形恰好与按票价从这120人中分层抽样所选的结果相同,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐地铁从A地到陶然亭的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s公里,试写出s的取值范围.(只需写出结论)
(本小题满分14分)如图,在五面体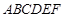 中,四边形
中,四边形 为正方形,
为正方形,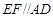 ,平面
,平面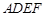
 平面
平面 ,且
,且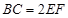 ,
,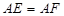 ,点G是EF的中点.
,点G是EF的中点.
(Ⅰ)证明: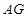
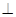
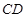 ;
;
(Ⅱ)若点 在线段
在线段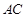 上,且
上,且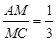 ,求证:
,求证: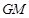 //平面
//平面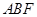 ;
;
(Ⅲ)已知空间中有一点O到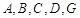 五点的距离相等,请指出点
五点的距离相等,请指出点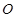 的位置. (只需写出结论)
的位置. (只需写出结论)
(本小题满分13分)已知等差数列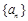 的前
的前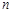 项和为
项和为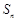 ,且满足
,且满足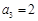 ,
,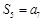 .
.
(Ⅰ)求数列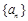 的通项公式
的通项公式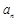 及
及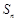 ;
;
(Ⅱ)若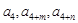 (
(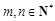 )成等比数列,求
)成等比数列,求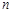 的最小值.
的最小值.
(本小题满分13分)已知点列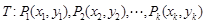 (
(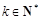 ,
,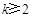 )满足
)满足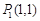 ,且
,且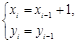 与
与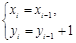 (
(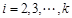 ) 中有且仅有一个成立.
) 中有且仅有一个成立.
(Ⅰ)写出满足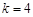 且
且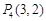 的所有点列;
的所有点列;
(Ⅱ) 证明:对于任意给定的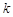 (
(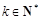 ,
,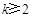 ),不存在点列
),不存在点列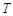 ,使得
,使得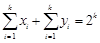 ;
;
(Ⅲ)当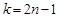 且
且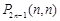 (
(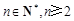 )时,求
)时,求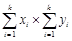 的最大值.
的最大值.