如图所示,AC和BC两轻绳共同悬挂一质量为8kg的物体,若保持AC绳的方向不变,AC与竖直向上方向的夹角为60°,BC绳的方向与竖直向上方向的夹角为θ且可以改变,(g=10N/kg)试求: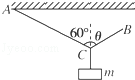
(1)当θ=600且物体平衡时,BC绳上的拉力大小;
(2)θ在0~90°的范围内,物体平衡时BC绳上拉力的最大值和最小值.
如下图甲所示,理想变压器原线圈通有正弦式交变电流,副线圈接有3个电阻和一个电容器。已知R1=R3=20Ω,R2=40Ω,原、副线圈的匝数比为10∶1,原线圈的输入功率为P=35W,已知通过R1的正弦交流电如下图乙所示。求:
(1)原线圈输入电压;
(2)电阻R2的电功率;
(3)电容器C流过的电流。
如图甲所示,一质量为m=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物体在受按如图乙所示规律变化的水平力F作用下向右运动,第3s末物块运动到B点时速度刚好为0,第5s末物块刚好回到A点,已知物块与粗糙水平间的动摩擦因数μ=0.2(g取10m/s2),求:
(1)AB间的距离;
(2)水平力F在5s时间内对物块的冲量。
如图甲所示,一个匝数n=100的圆形导体线圈,面积S1=0.4m2,电阻r=1Ω.在线圈中存在面积S2=0.3m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示.有一个R=2Ω的电阻,将其两端a、b分别与图甲中的圆形线圈相连接,求在0~4s时间内电阻R上产生的焦耳热.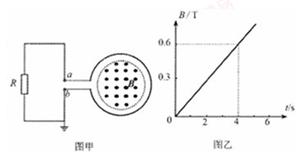
如图所示,图甲和图乙分别表示正弦脉冲波和方波的交变电流与时间的变化关系.若使这两种电流分别通过两个完全相同的电阻,求经过1min的时间,两电阻消耗的电功之比W甲:
W乙为多少.

如右图所示,光滑的水平面AB与半径为R="0.32" m的光滑竖直半圆轨道BCD在B点相切,D为轨道最高点.用轻质细线连接甲、乙两小球,中间夹一轻质弹簧,弹簧与甲、乙两球不拴接.甲球的质量为m1="0.1" kg,乙球的质量为m2="0.3" kg,甲、乙两球静止在光滑的水平面上。现固定甲球,烧断细线,乙球离开弹簧后进入半圆轨道恰好能通过D点。重力加速度g取10 m/s2,甲、乙两球可看作质点。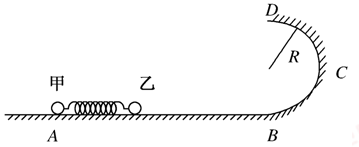
①试求细线烧断前弹簧的弹性势能;
②若甲球不固定,烧断细线,求乙球离开弹簧后进入半圆轨道能达到的最大高度;