（本题14分）如图，在平面直角坐标系中，抛物线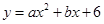
经过点A（-3，0）和点B（2，0）．直线y=h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F，与抛物线在第二象限交于点G．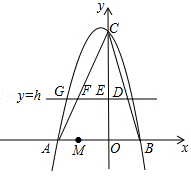
（1）求抛物线的解析式；
（2）连接BE，求h为何值时，△BDE的面积最大；
（3）已知一定点M（-2，0）．问：是否存在这样的直线y=h，使△OMF是等腰三角形？若存在，请求出h的值和点G的坐标；若不存在，请说明理由．
如图：学校旗杆附近有一斜坡．小明准备测量学校旗杆AB的高度，他发现当斜坡正对着太阳时，旗杆AB的影子恰好落在水平地面和斜坡的坡面上，此时小明测得水平地面上的影长BC=20米，斜坡坡面上的影长CD=8米，太阳光线AD与水平地面成30°角，斜坡CD与水平地面BC成30°的角，求旗杆AB的高度（结果保留根号）．
已知：如图，∠MAN=45°，B为AM上的一个定点， 若点P在射线AN上，以P为圆心，PA为半径的圆与射线AN的另一个交点为C，请确定⊙P的位置，使BC恰与⊙P相切.
（1）画出图形（不要求尺规作图，不要求写画法）；
（2）连结BP并填空：
① ∠ABC= °；
② 比较大小：∠ABP∠CBP.（用“＞”、“＜”或“=”连接）
如图,Rt△ABC的斜边AB=4，O是AB的中点，以O为圆心的半圆分别与两直角边相切于点D、E，
（1）求证∠A=∠B.
（2）求图中阴影部分的面积.
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC、AC于点D、E，连结EB交OD于点F．
（1）求证：OD⊥BE；
（2）若DE=
，AB=
，求AE的长．
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.
求证：△ADF∽△DEC；
若AB＝4，AD＝3
，AE＝3，求ED，AF的长.