(本小题满分12分)已知直线 ,
,
(1)若直线 过点(3,2)且
过点(3,2)且 ,求直线
,求直线 的方程;
的方程;
(2)若直线 过
过 与直线
与直线 的交点,且
的交点,且 ,求直线
,求直线 的方程.
的方程.
已知椭圆G的中心在坐标原点,长轴在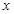 轴上,离心率为
轴上,离心率为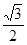 ,两个焦点分别为
,两个焦点分别为 和
和 ,椭圆G上一点到
,椭圆G上一点到 和
和 的距离之和为12.
的距离之和为12.
圆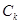 :
:
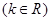 的圆心为点
的圆心为点 .
.
(1)求椭圆G的方程
(2)求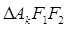 的面积
的面积
(3)问是否存在圆 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
已知集合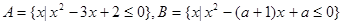
(1)当A=B时,求实数 的值;
的值;
(2)当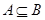 时,求实数
时,求实数 的取值范围。
的取值范围。
已知顶点在原点, 焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ,求抛物线的方程.
,求抛物线的方程.
如图正方体ABCD-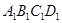 中,E、F、G分别是
中,E、F、G分别是 、AB、BC的中点.
、AB、BC的中点.
(1)证明: ⊥平面AEG;
⊥平面AEG;
(2)求 ,
,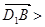

写出下列命题的否定:
(1)所有自然数的平方是正数
(2)任何实数x都是方程5x-12=0的根
(3)对于任意实数x,存在实数y,使x+y>0
(4)有些质数是奇数