某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20立方米时，按2元/立方米计费；月用水量超过20立方米时，其中的20立方米仍按2元/立方米收费，超过部分按2．6元/立方米计费．
（1）如果小红家每月用水15吨，水费是 元，如果每月用水23吨，水费是 元
（2）如果字母x表示小红家每月用水的吨数，那么小红家每月的水费如何用x代数式表示．
（3）如果小明家第二季度交纳水费的情况如下：
| 月份 |
四月份 |
五月份 |
六月份 |
| 交费金额 |
30元 |
34元 |
47．8元 |
小明家这个季度共用水多少立方米？
某粮店有大米a吨，第一天售出
，第二天售出余下的
.
（1）用代数式表示该粮店剩余大米数；
（2）当a=50时，求代数式的值.
.(14分)已知：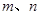
是方程
的两个实数根，且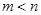
，抛物线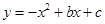
的图像经过点A(
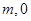)、B(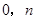
).
(1)求这个抛物线的解析式；(3分)
(2)设（1）中抛物线与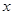
轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；(5分)
(3)P是线段OC上的一点，过点P作PH⊥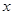轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标.(6分)
.(12分)如图1：⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在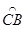
上取一点D，分别作直线CD、ED交直线AB于点F、M。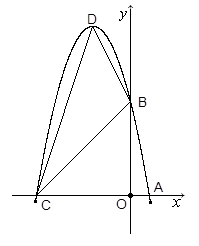
（1）求∠COA和∠FDM的度数；(3分)
（2）求证：△FDM∽△COM；(4分)
（3）如图2：若将垂足G改取为半径OB上任意一点，点D改取在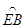
上，仍作直线CD、ED，分别交直线AB于点F、M，试判断：此时是否仍有△FDM∽△COM？证明你的结论。(5分)
(10分) 如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE. 
(1)DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；( 5分)
(2)若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。(5分)
(8分) 如图,用树状图或列表法求出下面两个转盘配成紫色的概率.(红色+蓝色=紫色)