如图1,在平面直角坐标系中,抛物线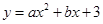 交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.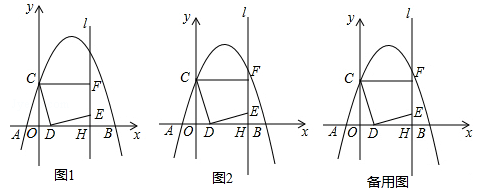
(1)求抛物线解析式;
(2)如图2,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:
①连接DF,求tan∠FDE的值;
②试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.
已知△ABC中,∠ACB=90°,AC=6,BC=8,过点A作直线MN⊥AC,点P是直线MN上的一个动点(与点A不重合),连结CP交AB于点D,设AP= ,AD=
,AD= .
.如图1,若点P在射线AM上,求y与x的函数解析式;

射线AM上是否存在一点P,使以点D、A、P组成的三角形与△ABC相似,若存在,求AP的长,若不存在,说明理由;
如图2,过点B作BE⊥MN,垂足为E,以C为圆心、AC为半径的⊙C与以P为圆心PD为半径的动⊙P相切,求⊙P的半径

电瓶厂投资2000万元安装了电动自行车电瓶流水线,生产的电瓶成本为40元只,设销售单价为 元(
元(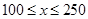 ),年销售量为
),年销售量为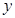 万件,年获利为
万件,年获利为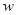 (万元).经过市场调研发现:当
(万元).经过市场调研发现:当 100元时,
100元时, 20万件.当100
20万件.当100
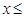 200元时,
200元时, 在100元的基础上每增加1元,
在100元的基础上每增加1元,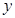 将减少0.1万件;当200
将减少0.1万件;当200
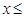 250元时,
250元时, 在200元的基础上每增加1元,
在200元的基础上每增加1元,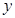 将减少0.2万件.(年获利
将减少0.2万件.(年获利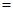 年销售额-生产成本-投资)
年销售额-生产成本-投资)当
 =180时,
=180时,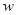 =▲万元;当
=▲万元;当 =240时,
=240时,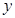 =▲万件
=▲万件求
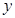 与
与 的函数关系式;
的函数关系式;当
 为何值时,第一年的年获利亏损最少?
为何值时,第一年的年获利亏损最少?
如图,一根电线杆AB和一块半圆形广告牌在太阳照射下,顶端A的影子刚好落在半圆形广告牌的最高处G,而半圆形广告牌的影子刚好落在地面上一点E.已知BC=5米,DE=2米,半圆的直径CD=6米.
求线段EF的长
求电线杆AB的高度
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.
求证:DE是⊙O的切线;
若AB=6,BD=3,求AE和BC的长.
如图,吴老师不小心把墨水滴在了3个班学生捐款金额的统计表上,只记得:三个班的捐款总金额是7700元,2班的捐款金额比3班的捐款金额多300元.
| 班级 |
1班 |
 2班 2班 |
3班 |
| 金额(元) |
2000 |
求2班、3班的捐款金额
若1班学生平均每人捐款的金额大于48元,小于51元.求1班的学生人数.