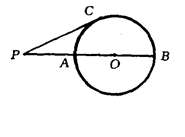
如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
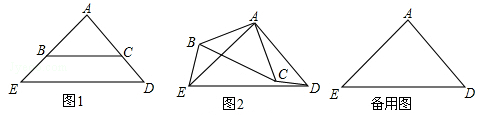
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=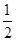 ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
如图所示,点 是⊙
是⊙ 上一点,⊙
上一点,⊙ 与⊙
与⊙ 相交于
相交于 、
、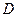 两点,
两点,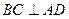 ,垂足为
,垂足为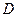 ,分别交⊙
,分别交⊙ 、⊙
、⊙ 于
于 、
、 两点,延长
两点,延长 交⊙
交⊙ 于
于 ,交
,交 的延长线于
的延长线于 ,
,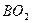 交
交 于
于 ,连结
,连结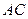 .
.求证:
 ;
;若
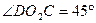 ,求证:
,求证: ;
; 若
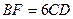 ,且线段
,且线段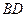 、
、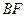 的长是关于
的长是关于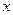 的方程
的方程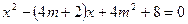 的两个实数根,求
的两个实数根,求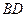 、
、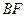 的长.
的长.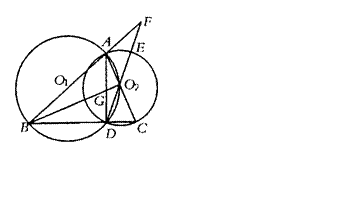
某公司投资新建了一商场,有商铺30间.据预测,当每间的年租金定为 万元时,可全部租出.若每间的年租金每增加
万元时,可全部租出.若每间的年租金每增加 元,则少租出商铺
元,则少租出商铺 间.该公司要为租出的商铺每间每年交各种费用
间.该公司要为租出的商铺每间每年交各种费用 万元,未租出的商铺每间每年交各种费用
万元,未租出的商铺每间每年交各种费用 元.
元.当每间商铺的年租金定为
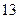 万元时,能租出多少间?
万元时,能租出多少间?当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为
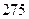 万元?
万元?
已知关于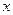 的一元二次方程
的一元二次方程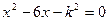 .
.求证:方程有两个不相等的实数根;
设
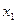 ,
,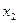 为方程的两个实数根,且
为方程的两个实数根,且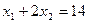 ,试求出方程的两个实数根和
,试求出方程的两个实数根和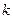 的值.
的值.
如图,以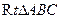 的直角边
的直角边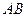 为直径的半圆
为直径的半圆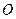 ,与斜边
,与斜边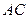 交于
交于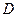 ,
,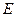 是
是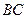 边上的中点. 连结
边上的中点. 连结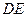 ,
,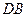 . 试问
. 试问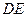 与半圆
与半圆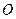 相切吗?若相切,请给出证明;若不相切,请说明理由.
相切吗?若相切,请给出证明;若不相切,请说明理由.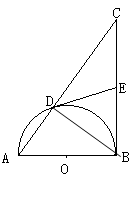
如图,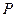 是⊙
是⊙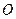 外一点,割线
外一点,割线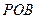 与⊙
与⊙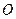 相交于
相交于 、
、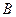 ,切线
,切线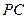 与⊙
与⊙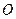 相切于
相切于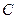 ,若
,若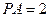 ,
,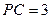 ,求⊙
,求⊙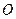 的半径.
的半径.