（1）如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1．8千米，AB=54米、BC=45米、AC=30米，求M、N两点之间的直线距离．
（2）列方程（组）或不等式（组）解应用题：2015年的5月20日是第15个中国学生营养日，我市某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如表）．
若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%，求这份快餐最多含有多少克的蛋白质？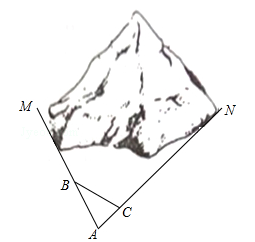
小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元：如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买了这种服装x件．
（1）当x= 时，小丽购买的这种服装的单价为76元；
（2）小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？
某校为了开阔学生的视野，积极组织学生参加课外读书活动．“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：
（1）求被调查的学生人数；
（2）补全条形统计图；
（3）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？
一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．
（1）从中任意摸出1个球，恰好摸到红球的概率是 ；
（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．
解方程：
（1）
；
（2）
；
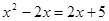（3）
．
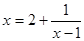如图，将一张长方形大铁皮切割（切痕为虚线）成九块，其中有两块是边长都为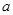
厘米的大正方形，两块是边长都为
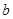厘米的小正方形，且
．
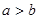（1）这张长方形大铁皮长为_____________厘米，宽为_____________厘米（用含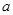、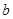的代数式表示）；
（2）①求这张长方形大铁皮的面积（用含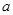、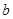的代数式表示）；
②若最中间的小长方形的周长为22厘米，大正方形与小正方形的面积之差为33平方厘米，试求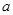和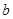的值，并求这张长方形大铁皮的面积．提示：
．
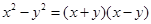（3）现要从切块中选择5块，恰好焊接成一个无盖的长方体盒子，共有哪几种方案可供选择（画出示意图）？按哪种方案焊接的长方体盒子的体积最大？试说明理由．（接痕的大小和铁皮的厚度忽略不计）