如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
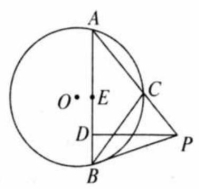
如图所示, 是 的一条弦, 是 外一点, 切 于点 , 交 于点 ,且 于点 是 的中点,求证: .
如图,已知 和 相交于 两点,过点 作 的切线交 于点 ,过点 作两圆的割线分别交 于点 与 相交于点 .
(1)求证: ;
(2)求证: ;
(3)当 与 为等圆时,且 时,求 与 的面积的比值.

已知等腰三角形 中, 的平分线与 边交于点 , 为 的内切圆 与 边的切点,作 ,交 于点 .
证明: 是 的切线.
如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 是 的直径,连接 .
(1)求证: ;
(2)若 于点 ,求 的值.

如图所示, 是 的直径,点 是 上不同的两点,直线 交线段 于点 ,交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.
